(See this post in another historical context: How do we know that atoms really exist?)
Here’s one way to think about it:
There are other ways to think about this. For instance, let’s call the sum ![]() :
:
![]()
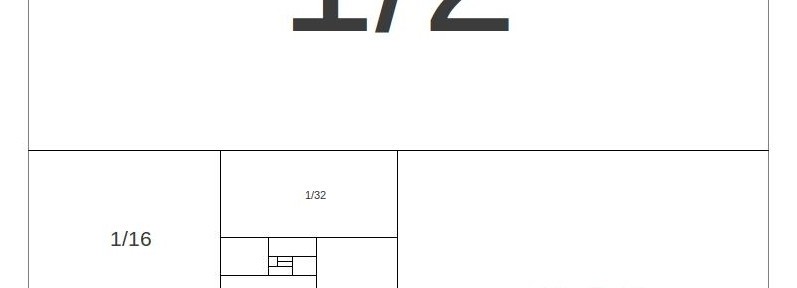
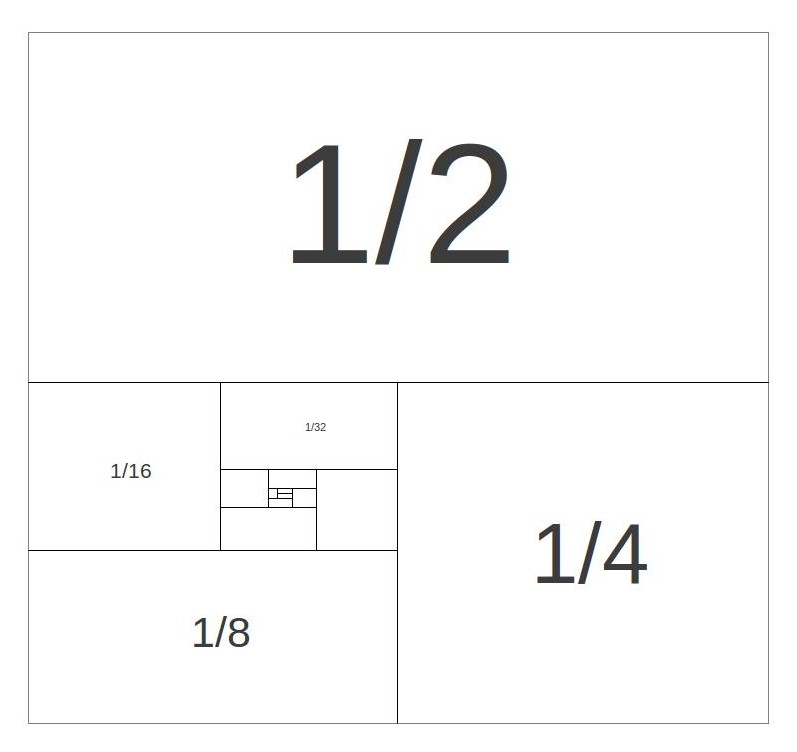
One thing that can be visualized in the diagram that might not be immediately obvious from the equation is that each number in the series is half of the preceding number. So instead of writing
![]()
we can write:
![]()
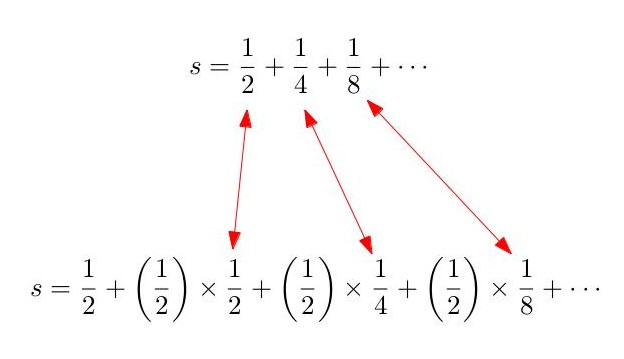
But now look at something:
The series shows up again! It’s just shifted to the right one place and every term is multiplied by ![]() :
:
![]()
This just means you can substitute the series itself back into the equation:
![]()
And we can solve this equation with simple algebra to get ![]() . This trick works any time you’re multiplying each number in a series by the same number. We can try it with
. This trick works any time you’re multiplying each number in a series by the same number. We can try it with ![]() :
:
![]()
![]()
![]()
![]()
which gives us ![]() . In fact, we can replace the multipliers
. In fact, we can replace the multipliers ![]() or
or ![]() with any number
with any number ![]() to get:
to get:
![]()
or, in other words,
![]()
We’ll call this the “geometric series formula.”
Let’s Get Pedantic
“So hold up, ![]() can be any number?” you say, incredulously.
can be any number?” you say, incredulously.
“Well, almost any number,” I say.
“What if I choose the number ![]() to be
to be ![]() ? Then the series goes
? Then the series goes ![]() If I group every two numbers together, I get
If I group every two numbers together, I get ![]() .”
.”
“Okay,” I say.
“But if I group the 2nd and 3rd together, and the 4th and 5th together, and leave the first out, I get ![]() .”
.”
“Hmm.”
“And if I do it your way, with the geometric series formula you just told me, I get:
![]()
So what gives?”
Alright, I may have overstated the case for my little formula just a tad. But let’s take a closer look at the series. If you just start adding terms together, you get ![]() after the first term,
after the first term, ![]() after the second term,
after the second term, ![]() after the third term, and so on. So in a sense,
after the third term, and so on. So in a sense, ![]() and
and ![]() are both acceptable answers, as the series oscillates back and forth between them. And even
are both acceptable answers, as the series oscillates back and forth between them. And even ![]() is kind of an acceptable answer, since it’s halfway between the two.
is kind of an acceptable answer, since it’s halfway between the two.
We can make this notion more precise. Looking at the new sequence generated by adding succesive terms of the series together: ![]() , we can average the terms of this sequence to get a new sequence:
, we can average the terms of this sequence to get a new sequence: ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and so forth. This sequence does converge to
, and so forth. This sequence does converge to ![]() , meaning that, as we expected, the average value of the series
, meaning that, as we expected, the average value of the series ![]() is
is ![]() . This idea of averaging terms of a series which oscillates back and forth indefinitely is called Cesaro summation, after Ernesto Cesaro, a 19th century Italian mathematician. It turns out that, as long as it’s not infinite, the Cesaro sum will always equal the result of the geometric series formula derived in the first section.
. This idea of averaging terms of a series which oscillates back and forth indefinitely is called Cesaro summation, after Ernesto Cesaro, a 19th century Italian mathematician. It turns out that, as long as it’s not infinite, the Cesaro sum will always equal the result of the geometric series formula derived in the first section.
“But what about…”
“Alright,” you say, “that was a one-off case. What if, instead of choosing ![]() , we chose
, we chose ![]() ? Then we get
? Then we get ![]() , which clearly doesn’t bounce back and forth like the other series. You can’t even average the values together, because the series keeps growing and growing. (Mathematicians would say that this series is not Cesaro summable, or that the Cesaro sum is infinite). But if we use the geometric series formula, we get:
, which clearly doesn’t bounce back and forth like the other series. You can’t even average the values together, because the series keeps growing and growing. (Mathematicians would say that this series is not Cesaro summable, or that the Cesaro sum is infinite). But if we use the geometric series formula, we get:
![]()
So you’re telling me that if we start adding together bigger and bigger positive numbers, and never subtract or add negative numbers, and the series always gets bigger and bigger, that all of those sums added together will give us ![]() ? Tell me the truth; you’re just making this up as you go along.”
? Tell me the truth; you’re just making this up as you go along.”
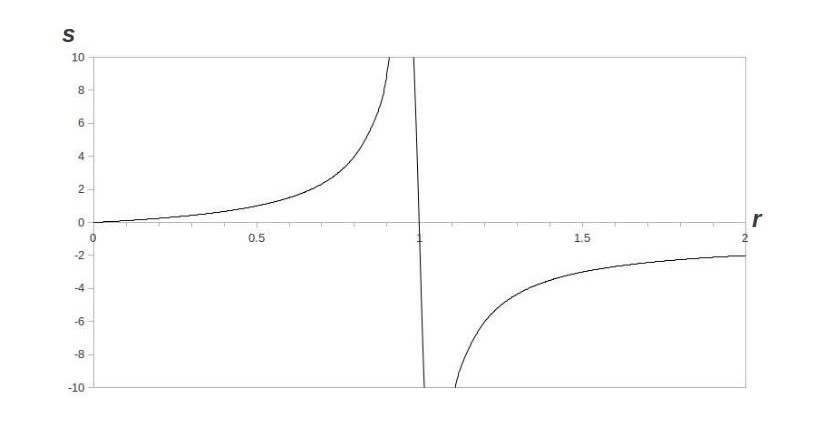
This is precisely what Leibniz and Euler were doing in the 17th and 18th centuries. Leibniz was happy to accept the geometric series formula as gospel, but Euler looked for a deeper explanation. He, too, had a hard time denying the power of the geometric series formula in other situations like the one we mentioned in the previous section. He thought about the graph of the formula ![]() :
:
For our standard converging geometric series, as ![]() gets closer and closer to
gets closer and closer to ![]() from below, the sum gets bigger and bigger (just as the series for
from below, the sum gets bigger and bigger (just as the series for ![]() has a bigger sum than
has a bigger sum than ![]() ). Eventually, the sum goes to infinity and then “wraps around” to negative infinity, at which point it begins to get smaller. Euler reckoned that this process was exactly what was happening with the series
). Eventually, the sum goes to infinity and then “wraps around” to negative infinity, at which point it begins to get smaller. Euler reckoned that this process was exactly what was happening with the series ![]() , that the numbers were getting so big, they were “wrapping around” infinity to negative infinity and coming out the other side to become negative. This is how he reasoned that the sum of ever-increasing positive numbers would give a negative number. He even figured out a formula to do this for all sorts of series. We call this formula an Euler summation. For geometric series, the Euler sum is always the same as the geometric series formula.
, that the numbers were getting so big, they were “wrapping around” infinity to negative infinity and coming out the other side to become negative. This is how he reasoned that the sum of ever-increasing positive numbers would give a negative number. He even figured out a formula to do this for all sorts of series. We call this formula an Euler summation. For geometric series, the Euler sum is always the same as the geometric series formula.
“Alright, smart guy, one more”
“Okay, that last one was really reaching, but I’ll let it slide for now. But what about ![]() ? Even Euler can’t deny that
? Even Euler can’t deny that ![]() , and every math teacher I’ve ever had tells me that you can’t divide by zero. Ha! I finally have you!”
, and every math teacher I’ve ever had tells me that you can’t divide by zero. Ha! I finally have you!”
It’s true, the geometric series has run out of tricks and is no longer of use to us. The Cesaro sum is infinite and the Euler sum doesn’t exist. Is there any way to make sense of this series? Well, first of all, let’s take a look at what the series looks like. If the first term is ![]() and each successive term is just the preceding term multiplied by
and each successive term is just the preceding term multiplied by ![]() , then the series is just
, then the series is just ![]() So can it be summed?
So can it be summed?
Amazingly, it can! The groundwork was laid by Euler and later by Riemann, who were studying sums of the form:
![]()
or, in more modern notation:
![Rendered by QuickLaTeX.com \[ \zeta(x)=\sum_{n=1}^{\infty}\frac{1}{n^x} \]](http://www.howdoweknowit.com/wp-content/ql-cache/quicklatex.com-fe7470dde29560353fe0ec6568880afe_l3.png)
This is known as the Riemann zeta function, and it has incredibly deep properties that, even after 2 centuries, mathematicians are still trying to unravel. For our purposes, it suffices to recognize that our series is just what happens when you set ![]() in the Riemann zeta function:
in the Riemann zeta function:
![]()
Since any number to the zero power is 1, by plugging in zero for all the powers, we get back our original series ![]() Now the only question is how we evaluate the Riemann zeta function at
Now the only question is how we evaluate the Riemann zeta function at ![]() .
.
It would be nice if we could relate this series to another series that we know how to sum. For instance, our current series, ![]() , looks a lot like the series
, looks a lot like the series ![]() , which we know has a Cesaro sum of
, which we know has a Cesaro sum of ![]() . We’ll actually consider another very closely related series,
. We’ll actually consider another very closely related series, ![]() , which bounces back and forth between
, which bounces back and forth between ![]() and
and ![]() and has a Cesaro sum of
and has a Cesaro sum of ![]() . So how do we turn the first series into the second series? Like this:
. So how do we turn the first series into the second series? Like this:
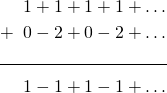
The first series is just ![]() . We can take all the zeros out of the second series to get
. We can take all the zeros out of the second series to get ![]() . And we mentioned earlier that the series
. And we mentioned earlier that the series ![]() is Cesaro summable to
is Cesaro summable to ![]() . So we have the equation:
. So we have the equation:
![]()
which we can solve to get ![]() .
.
Why it matters
We’ve seen that mathematicians over the years have come up with ways to add up infinite sets of numbers with varying degrees of success and plausibility. But a lot of this seems counterintuitive. You might reasonably ask whether the math that we’ve done here has any bearing on the real world. In fact, it does, in a technique called renormalization that’s used by physicists today. It turns out that a lot of important theories in physics generate series like the ones above. If we were to naively add up these series, we would get really weird results, like electrons with infinite electric charge. Physicists can use procedures like the ones we’ve mentioned here to get results that make sense and make reasonable predictions that can be tested. But many physicists are suspicious of these methods and hypothesize that there’s a deeper reason that we don’t yet understand for why this math works. For now, these methods allow us to tackle important physical problems, in addition to being the key to how we know that ![]() .
.
References
- E. Sandifer, “Divergent Series.” How Euler Did It. Mathematical Association of America, June 2006. Retrieved from http://www.maa.org/news/howeulerdidit.html on 7 Dec 2012.