How Do We Know It? Festivus Special Edition

The Airing of Grievances

At some point in our lives, most scientists have to deal with gross misconceptions about exactly what it is that we do. Upon learning that I’m a chemist, people typically ask me two questions in rapid fire succession: “Can you make bombs?” and “Can you make drugs?” This hasn’t just happened to me a few times; I’m batting well over .500 with those two questions. And it’s not like I’m constantly introducing myself to anarchists and tweakers. I tend to assume that those are the two questions I get because they’re the most intriguing topics to a non-chemist. For most chemists, though, it’s bad when things explode, and drugs are less interesting for recreational purposes and more interesting on a fundamental level in how they enhance or suppress certain biochemical pathways and then people’s eyes glaze over and I realize I’ve essentially been talking to myself for 15 minutes. I’ve learned to accept that I’ll get these two questions and that my answers to them will be profoundly uninteresting to my interrogators.

"Needs more quicksilver." — “Needs more quicksilver.”

Most of the rest of the people I meet haven’t the slightest clue what chemists do or what chemistry even is. They just assume I throw random chemicals together waiting for something to happen (which isn’t far from the truth, but hey, I’m trying to maintain my dignity here). To most people, chemistry is much the same as it was in the Dark Ages, with bedraggled folks spending long days in their labs immersed in a haze of brimstone and quicksilver, poring over inscrutable alchemical treatises yellowed with age and acid (again, not far from the truth). If they took chemistry at all in high school or college, their most common line is “God I hated chemistry. Like couldn’t stand it.” Chemistry may or may not be the most frequently hated high school class, but it certainly seems like it’s the most vehemently hated one.

Then there are the select few that have just enough education in the subject to be dangerous. They’ll usually brag about the fact that they did well in chemistry but didn’t really find it all that interesting. Inevitably, they get caught up with the magic word, “stoichiometry.” I don’t know if they just like saying it because it’s a big word, or if they honestly think that chemistry begins and ends with stoichiometry. I can assure you of this: I do very little stoichiometry in my average day as a practicing chemist. Like, almost none. Nonetheless, these folks will talk about how tough balancing equations was when they were taking chemistry, but they always seemed to manage to pull it off. I guess maybe it’s bragging rights; stoichiometry as it’s taught in schools is usually taught pretty pitifully, and it’s made to look a hell of a lot harder than it is. You can already see where this is going. It’s time for…

Feats of Strength

Betcha didn’t know I was gonna rope you into a stoichiometry lesson. If you’re in high school or college taking intro chemistry right now, sit down, strap in, and thank your lucky stars, because this is the last stoichiometry lesson you’ll ever need. To get a feel for the method we’ll be using, I’ll start with a really simple equation:

$H_2 + O_2 \longrightarrow H_{2}O$

Now, this equation isn’t balanced, so let’s throw in some coefficients to balance it. But since we don’t know what those coefficients are yet, let’s just throw in some variables:

$x~H_2 + y~O_2 \longrightarrow z~H_{2}O$

Each of the elements (hydrogen and oxygen) is going to give us a clue as to what the identities of $x$ , $y$ , and $z$ are. So we start with hydrogen (H): there are 2 H’s associated with $x$ , no H’s associated with $y$ , and 2 H’s associated with $z$ . We can write this as:

$2x+0y&=2z$

$\begin{align*} 2x&=2z\\ x&=z \end{align*}$

So already we know that the number in front of $H_2$ ( $x$ ) is going to equal the number in front of $H_{2}O$ ( $z$ ). Now we move to oxygen (O): there are no O’s associated with $x$ , 2 O’s associated with $y$ , and 1 O associated with $z$ . This gives us:

$\begin{align*} 0x+2y&=z\\ 2y&=z \end{align*}$

Now we know that the number in front of $H_{2}O$ ( $z$ ) is twice as big as the number in front of $O_2$ ( $y$ ). Combining this information with the information we got from the H’s, we have:

$x=2y=z$

Now, we can choose any number we want for $x$ and get out numbers for $y$ and $z$ that will make the equation balanced. If we choose $x=1$ , for example, we get $y=\frac{1}{2}$ and $z=1$ , or plugging those back into our original chemical equation:

$1~H_2 + \frac{1}{2}~O_2 \longrightarrow 1~H_{2}O$

which is a perfectly valid and balanced chemical equation. Now, you might have sticklers for teachers who tell you that the numbers in front of your equations should be whole numbers, in which case you can multiply the whole equation by two to get the more familiar:

$2~H_2 + O_2 \longrightarrow 2~H_{2}O$

But either one is a valid balanced chemical equation. It’s a Festivus miracle!

Now, obviously I chose a really easy equation to balance so that I could show you how the method works. But it works regardless of how complicated the equation. Let’s try another one real quick. I’ll try to explain what’s going on as we go:

$a~C_{8}H_{18}+b~O_{2} \longrightarrow c~H_{2}O+d~CO_{2}$

We collect each element individually as we did above, starting with the C’s:

$\begin{align*} 8a+0b&=0c+d\\ 8a&=d \end{align*}$

Do the same thing with H:

$\begin{align*} 18a+0b&=2c+0d\\ 9a&=c \end{align*}$

And finally O:

$2b=c+2d$

A balanced chemical equation is just shorthand for a system of algebraic equations, like the ones above. You may notice that we have four variables, $a$ , $b$ , $c$ , and $d$ , but only three equations. This is what is called an underdetermined system, which means that there’s no unique solution to the problem. However, we can determine a family of solutions, all of which produce a properly balanced equation. All we have to do is get one big continuous equation for $a$ , $b$ , $c$ , and $d$ like we did for $x$ , $y$ , and $z$ in the first example. Our current example is already off to a good start, as we have $8a=d$ and $9a=c$ at the outset. So we have:

$\begin{align*} 9a&=c\\ a&=\frac{1}{9}c\\ 8a&=d\\ \frac{8}{9}c&=d=8a \end{align*}$

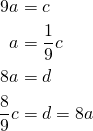
Now all we have to do is figure out a way to get $b$ into this chain and we’ve solved the equation.

$2b=c+2d$

Substituting for $c$ and $d$ ,

$\begin{align*} 2b&=9a+16a=25a\\ a&=\frac{2}{25}b \end{align*}$

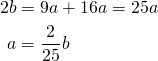
Putting all the pieces together gives us:

$8a=\frac{16}{25}b=\frac{8}{9}c=d$

As we said before, the equation above gives us a family of solutions, basically a rule for balancing the equation. If we just plug in $a=1$ , we get $b=\frac{25}{2}$ , $c=9$ , $d=8$ , or:

$C_{8}H_{18}+\frac{25}{2}~O_{2} \longrightarrow 9~H_{2}O+8~CO_{2}$

which is balanced. If your teacher’s a real stickler and hates fractions for some reason, you can always just multiply the whole thing by two so that all your coefficients are whole numbers.

Here’s one with a little twist:

$ICl+H_{2}S_{2}O_{7} \longrightarrow I_{2}^+ + I(HSO_{4})_{3} + HS_{3}O_{10}^- + HSO_{3}Cl + H_{2}SO_{4}$

This one’s from my advanced inorganic chem book from college. It’s a monster if you try doing it the trial-and-error way everyone learns in high school. But let’s try it with the method that I just described:

$\begin{align*} a~ICl+b~H_{2}S_{2}O_{7} \rightarrow c~I_{2}^+ +~ &d~I(HSO_{4})_{3} + e~HS_{3}O_{10}^-\\ &+ f~HSO_{3}Cl + g~H_{2}SO_{4} \end{align*}$

Now if we collect the iodines (I):

$\begin{align*} 1a+0b&=2c+1d+0e+0f+0g\\ a&=2c+d \end{align*}$

Collecting chlorines (Cl) next:

$\begin{align*} 1a+0b&=0c+0d+0e+1f+0g\\ a&=f \end{align*}$

Repeating the process, we get the following equations for H, S, and O:

$2b=3d+e+f+2g$

$2b=3d+3e+f+g$

$7b=12d+10e+3f+4g$

Now, you may notice that we have seven variables, but only five equations listed here. This system is too underdetermined to even get a family of solutions. So what gives? Is it just not possible to balance this equation? In fact, we can balance this equation; we’ve just overlooked another constraint on the system. If you look at the original equation, the $c$ term has a positive charge and the $e$ term has a negative charge. You’ll also notice that the reactants are uncharged (the total charge on the reactants is zero). Since charge is conserved in chemical reactions, you know that the total charge on the products have to be zero. This means that there has to be as much positive charge as negative charge. In order for this to be the case, we must have $c=e$ . This gives us our sixth equation and lets us use our method to balance the chemical equation. I won’t go through all the nitty gritty math, but the equation you should get in the end is:

$a=\frac{5}{9}b=\frac{5}{2}c=5d=\frac{5}{2}e=f=\frac{5}{4}g$

You can just plug in $a=1$ to get all the rest of the coefficients. As we’ve seen, that’ll give you a balanced equation. But if you want all the coefficients to be whole numbers, you can plug in $d=1$ . That gives you $a=5$ , $b=9$ , $c=2$ , $e=2$ , $f=5$ , and $g=4$ , or: