In the first part of this post, I explained how scientists found out in the late 18th century that diamond, graphite, and charcoal were all made of carbon. As a quick explanation of how such different materials could be made of the same element, I put up the following photo, showing that diamond and graphite actually have vastly different structures:
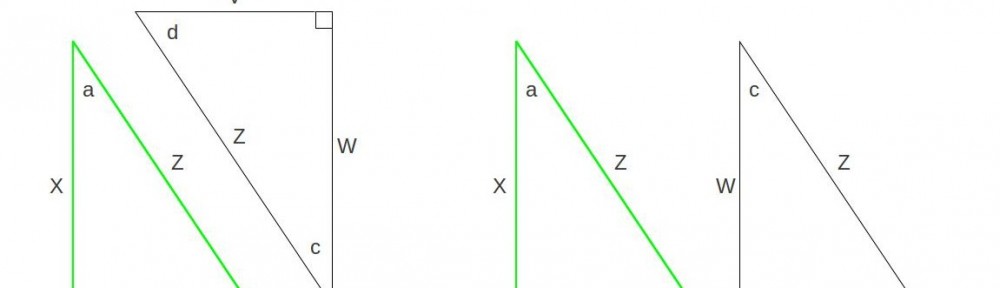
I know I promised last time that I’d explain how we know about the different structures of diamond and graphite, but that one’s not quite ready yet. Plus, the last post was really long, so I figured I’d give your brain a little rest and do some high-school geometry (some of you might not consider that a “rest,” but I promise to make it as painless as I can). The fact that you can unfold a triangle to make a straight line (180 degrees) has been known since ancient times, and it’s been the subject of some really ingenious proofs and some fundamental advances in math over the years. I wanted to take a moment to present you with two proofs: one that I just made up on the fly, and one from Euclid. The proofs are neat, and they give some insight into how mathematicians think about problems; but more importantly, I’ve got a couple of other HDWKI’s planned that will use some of these properties of triangles, so it helps to have a decent understanding of them now, so those posts don’t stretch on to eternity.
@HDWKI is now on Twitter! Follow me by clicking the widget at the top right sidebar of the home page.
“Thus there is not merely one world, one earth, one sun, but as many worlds as we see bright lights around us…”