I know I promised last time that I’d explain how we know about the different structures of diamond and graphite, but that one’s not quite ready yet. Plus, the last post was really long, so I figured I’d give your brain a little rest and do some high-school geometry (some of you might not consider that a “rest,” but I promise to make it as painless as I can). The fact that you can unfold a triangle to make a straight line (180 degrees) has been known since ancient times, and it’s been the subject of some really ingenious proofs and some fundamental advances in math over the years. I wanted to take a moment to present you with two proofs: one that I just made up on the fly, and one from Euclid. The proofs are neat, and they give some insight into how mathematicians think about problems; but more importantly, I’ve got a couple of other HDWKI’s planned that will use some of these properties of triangles, so it helps to have a decent understanding of them now, so those posts don’t stretch on to eternity.
Who even cares about this question?
The question that kicked off this blog post implies that we already know the answer. Otherwise, how would we know to ask that question at all? How does a mathematician even figure out what questions to ask in the first place? Well, in this case, we can make up a scenario where a mathematician is doing a lot of work with triangles (maybe she’s also a surveyor or architect). Let’s say she needs to figure out a certain angle for a building she’s working on. Just to save time (in case she has to figure out more angles later), she whips out her protractor and proceeds to measure every angle in the blueprint. She notices by chance that one triangle’s angles add up to 180. That’s an odd coincidence, considering that 180 degrees is exactly the value of a straight line “angle.” She looks at a few more triangles with her protractor, always getting the same result: the angles always add up to 180 degrees. “Ok, this is weird,” she might think, and now she may start to wonder if that’s always the case–if it’s just a feature of triangles in general. That’s one way that she may get around to asking the question at the top of this post.
Alright, now that we know where the question may have come from, let’s prove the damn thing already. You might want to get a pencil and paper to follow along. First, my proof. I don’t claim any novelty or originality here; I’m sure plenty of people have figured this proof out over the years, but it’s what I came up with on the fly. I will claim some degree of originality in the presentation, though. See, one of the biggest difficulties in learning math is being shown step-by-step how to get from the question to the answer, without ever being shown how to come up with those steps. I want to try to explain how I came up with this proof. So fair warning; if my explanation feels a little disjointed, it’s because it’s a reflection of how I was actually figuring this problem out. I’ll do the same thing with Euclid’s proof, too, showing how he might have figured it out.
The proof (for real this time)
The first thing I noticed was that 180 is an easy number to work with in geometry, since it’s the angle of a straight line (this is reflected in our language: we say someone “does a complete 180” when they reverse their position on something). It’s also the sum of two right angles (90 degrees each). With that many right angles, I thought, “why don’t we put the triangle in a box? That way we’ll already know at least some of the angles we’re working with.”
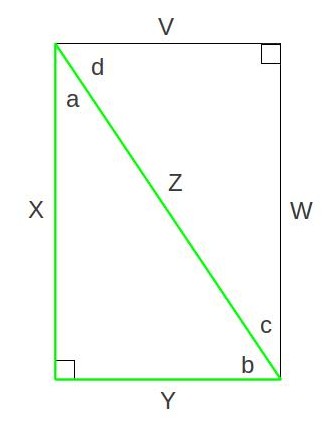
 So here’s a random triangle (in green) inside a rectangle. I’ve labeled all the angles. We want to show that
So here’s a random triangle (in green) inside a rectangle. I’ve labeled all the angles. We want to show that ![]() . We know that all the corners of the rectangle are 90 degrees by definition. So that tells us that
. We know that all the corners of the rectangle are 90 degrees by definition. So that tells us that ![]() and
and ![]() . We also know that a straight line is 180 degrees, so that means
. We also know that a straight line is 180 degrees, so that means ![]() . What can we do with this information? Well, not much, but we might notice that the green triangle isn’t the only one inside the rectangle. In particular, we might look at two other triangles:
. What can we do with this information? Well, not much, but we might notice that the green triangle isn’t the only one inside the rectangle. In particular, we might look at two other triangles:
 The blue and red triangles are both right triangles, and at this point you might think, “Hey, we already know one angle in a right triangle is 90 degrees. So maybe it’s easier to prove that the angles in a right triangle add up to 180. And if we can prove that, it’ll give us a little more information about how to figure out what
The blue and red triangles are both right triangles, and at this point you might think, “Hey, we already know one angle in a right triangle is 90 degrees. So maybe it’s easier to prove that the angles in a right triangle add up to 180. And if we can prove that, it’ll give us a little more information about how to figure out what ![]() is in the picture above.”
is in the picture above.”
So how do we calculate the sum of the angles in a right triangle? Well, since a right triangle already has a right angle, we can think of putting itin a box as well:
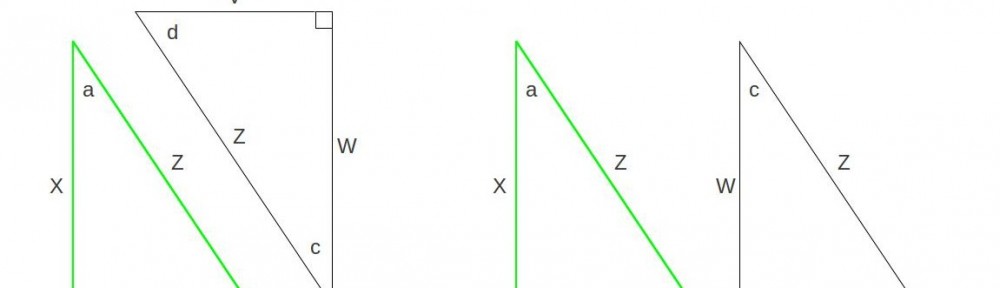
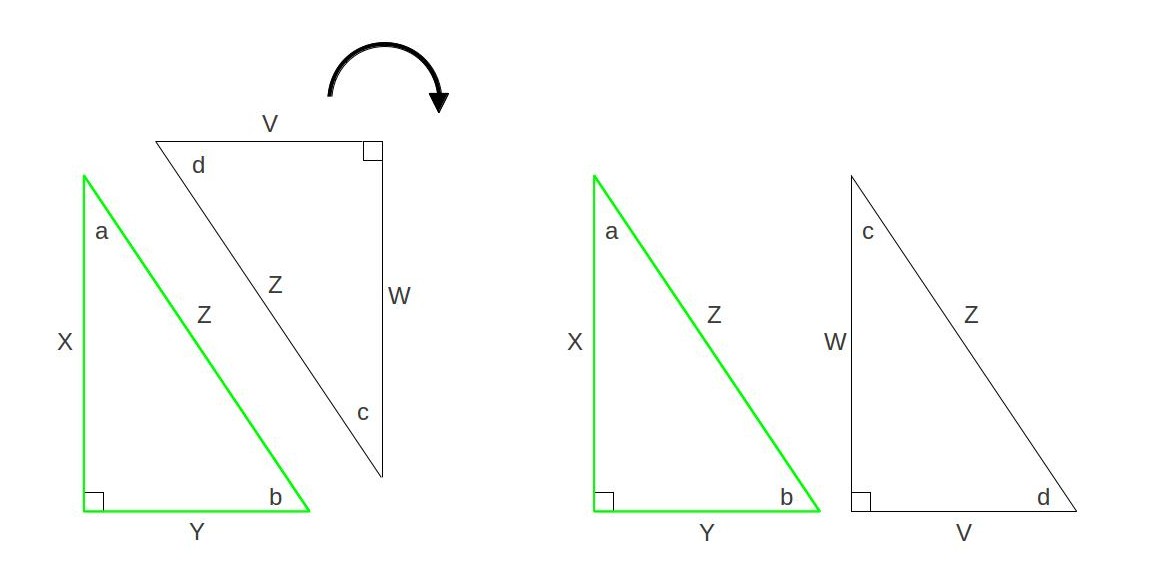
 I’ve gone ahead and labeled all the angles and sides. We can see that the original right triangle, highlighted in green, fits snugly in the corner of the box. It’s got the sides labeled
I’ve gone ahead and labeled all the angles and sides. We can see that the original right triangle, highlighted in green, fits snugly in the corner of the box. It’s got the sides labeled ![]() ,
, ![]() , and
, and ![]() . We also can see that angles
. We also can see that angles ![]() and
and ![]() form a corner of the box, as do angles
form a corner of the box, as do angles ![]() and
and ![]() . This tells us that
. This tells us that ![]() degrees. The real trick comes in seeing the other triangle: the one with sides labeled
degrees. The real trick comes in seeing the other triangle: the one with sides labeled ![]() ,
, ![]() , and
, and ![]() . Since we’re dealing with a rectangle, we know that
. Since we’re dealing with a rectangle, we know that ![]() and
and ![]() . But wait, that means that all three sides are equal to the three sides of the green triangle. If we turn the black triangle upside down, we can see that the black triangle and the green triangle are actually identical:
. But wait, that means that all three sides are equal to the three sides of the green triangle. If we turn the black triangle upside down, we can see that the black triangle and the green triangle are actually identical:
 This means that the angle
This means that the angle ![]() is the same as the angle
is the same as the angle ![]() , and the angle
, and the angle ![]() is the same as angle
is the same as angle ![]() . But we know that
. But we know that ![]() , so if
, so if ![]() , then that means
, then that means ![]() , and since the other corner is 90 degrees as well, we’ve shown that the angles of a right triangle add up to 180 degrees!
, and since the other corner is 90 degrees as well, we’ve shown that the angles of a right triangle add up to 180 degrees!
Ok, so what does this mean for our original triangle? Let’s take another look at it.
 From before, we knew that
From before, we knew that ![]() and
and ![]() because they were in the corners of the box. Now, knowing what we do about right triangles, we can say that
because they were in the corners of the box. Now, knowing what we do about right triangles, we can say that ![]() and
and ![]() . But if
. But if ![]() and
and ![]() , then that means that
, then that means that ![]() has to be equal to
has to be equal to ![]() . The plot thickens… And if
. The plot thickens… And if ![]() and
and ![]() , then
, then ![]() has to be equal to
has to be equal to ![]() . Curiouser and curiouser… So now we have
. Curiouser and curiouser… So now we have ![]() and
and ![]() . But that means that
. But that means that ![]() , too. Ok, well what else do we know about
, too. Ok, well what else do we know about ![]() ? We know that
? We know that ![]() makes a straight line, so that means that
makes a straight line, so that means that ![]() . But since
. But since ![]() , that also means that
, that also means that ![]() . And that’s how we know that the angles of a triangle add up to 180 degrees. When it rains, it pours. You might want to take a few minutes to really go over this last little bit, as it all happens pretty quickly. But it’s pretty neat how you have nothing, nothing, nothing, and then you notice one little thing about right triangles and your answer practically jumps out of the screen and screams at you.
. And that’s how we know that the angles of a triangle add up to 180 degrees. When it rains, it pours. You might want to take a few minutes to really go over this last little bit, as it all happens pretty quickly. But it’s pretty neat how you have nothing, nothing, nothing, and then you notice one little thing about right triangles and your answer practically jumps out of the screen and screams at you.
Euclid’s Proof
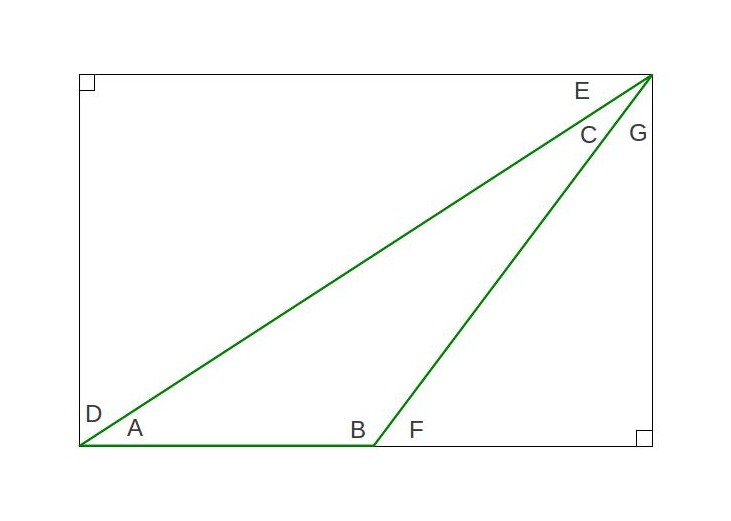
Alright, I promised I’d show you how Euclid proved this. Euclid’s kind of a badass, in a weird way. His geometry book, The Elements, is so good that it was the standard geometry textbook in the western world for over 2000 years–that is, until publishers realized that they could just release slightly altered editions of textbooks each year and make truckloads of money. Aaaaaaaaaaaanyways, here goes. Euclid thought of the problem by extending the triangles sides beyond their corners:
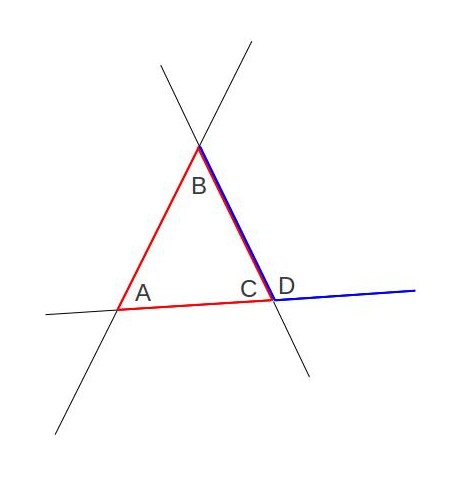 Our generic triangle is in red. I’ve also highlighted another angle,
Our generic triangle is in red. I’ve also highlighted another angle, ![]() , in blue. Euclid knew that the angles
, in blue. Euclid knew that the angles ![]() and
and ![]() add up to give you a straight line, or 180 degrees. This means that if you can show
add up to give you a straight line, or 180 degrees. This means that if you can show ![]() , then you can show that the angles of a triangle add up to 180. To do that, Euclid drew another line, parallel to the side of the triangle opposite angle
, then you can show that the angles of a triangle add up to 180. To do that, Euclid drew another line, parallel to the side of the triangle opposite angle ![]() :
:
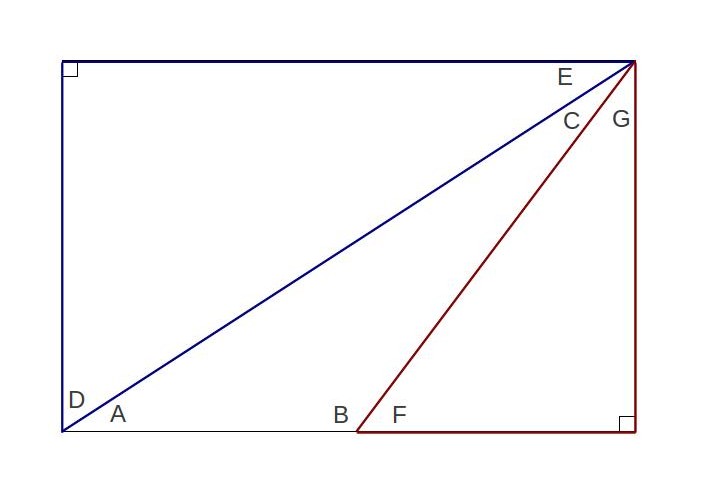
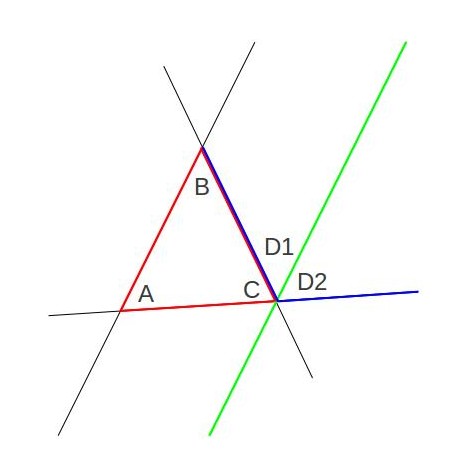 The green line is the new parallel line. One thing to notice is that the angle
The green line is the new parallel line. One thing to notice is that the angle ![]() and the angle
and the angle ![]() are the same. The reason they’re the same is because the line they’re on crosses two parallel lines. I’ve tried to highlight that fact in this picture to make it easier to see:
are the same. The reason they’re the same is because the line they’re on crosses two parallel lines. I’ve tried to highlight that fact in this picture to make it easier to see:
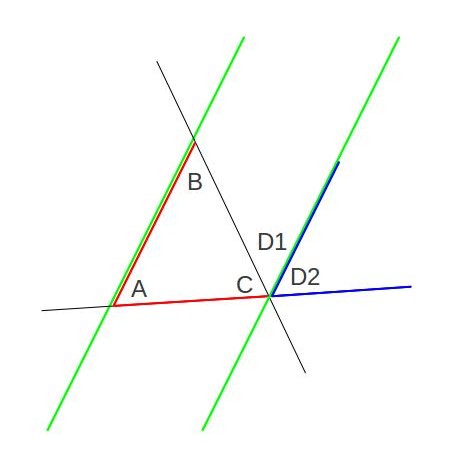 Since the two green lines are parallel, if one line intersects them both, it has to do so at the same angle. So that means that
Since the two green lines are parallel, if one line intersects them both, it has to do so at the same angle. So that means that ![]() , as we said before. So where does that leave us now? We know that
, as we said before. So where does that leave us now? We know that ![]() and
and ![]() . This means that
. This means that ![]() . We’re trying to show that
. We’re trying to show that ![]() . So all we need to do now is show that
. So all we need to do now is show that ![]() and we’ll be done. So take a look at this next picture:
and we’ll be done. So take a look at this next picture:
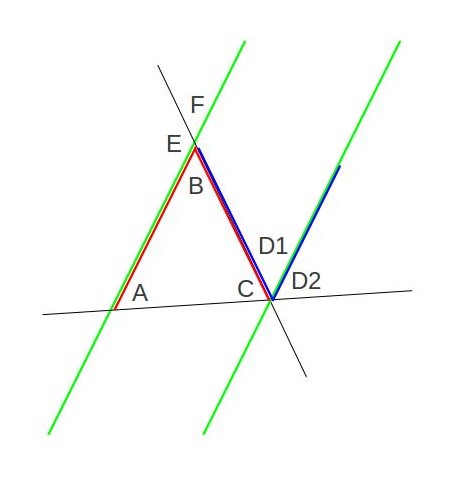 I’ve highlighted angles
I’ve highlighted angles ![]() and
and ![]() . I’ve also labeled angle
. I’ve also labeled angle ![]() , and since the line with
, and since the line with ![]() ,
, ![]() , and
, and ![]() crosses the two parallel green lines, that means that
crosses the two parallel green lines, that means that ![]() , for the same reason that we said
, for the same reason that we said ![]() above. Now, we’re trying to show that
above. Now, we’re trying to show that ![]() to complete our proof, but with this new bit of information, all we need to do now is show that
to complete our proof, but with this new bit of information, all we need to do now is show that ![]() and we’ll be done. How do we do that? I’ve erased most of the extra lines to make the picture below:
and we’ll be done. How do we do that? I’ve erased most of the extra lines to make the picture below:
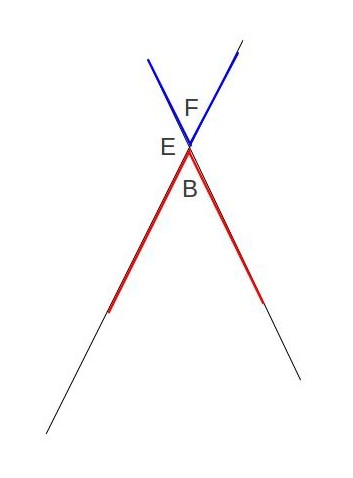 Now we just have the relevant part of the picture. We can see that
Now we just have the relevant part of the picture. We can see that ![]() and
and ![]() form a straight line, and that
form a straight line, and that ![]() and
and ![]() form another straight line. But this just means that
form another straight line. But this just means that ![]() , and
, and ![]() . But for that to be true,
. But for that to be true, ![]() has to equal
has to equal ![]() . So if
. So if ![]() ,
, ![]() , and
, and ![]() , then that means that
, then that means that ![]() and we’re done. Euclid’s proof is a bit cleverer than mine, but the neat thing to take away from this is that there are often multiple roads to the same answer.
and we’re done. Euclid’s proof is a bit cleverer than mine, but the neat thing to take away from this is that there are often multiple roads to the same answer.
Is that all there is?
So you may naturally ask the question, “Is there ever a case where the angles in a triangle don’t add up to 180 degrees?” The surprising answer is yes, although you can’t do it on a flat sheet of paper. I won’t go into too much detail here, but if you try to draw a triangle on a curved surface, such as a sphere, you end up finding that the angles don’t add up to 180 degrees. This is important for figuring out placement of various features on a globe, for example, and for navigation on a curved surface (like the surface of the Earth). Triangles of this sort weren’t anticipated by Euclid, and are generally referred to as non-Euclidean. I’ll leave you with just one example, possibly the most famous triangle in the world whose angles don’t add up to 180 degrees:
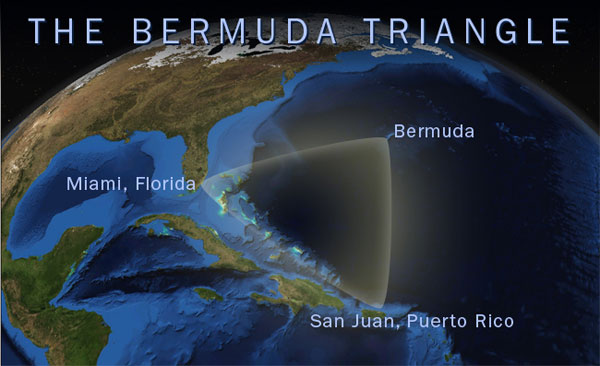
See what happens when you don’t listed to Euclid?
References
David Joyce maintains a brilliant site with Euclid’s classic textbook, Elements. His site also includes explanations and interactive materials. Really great if you want to geek out on geometry:
- http://aleph0.clarku.edu/~djoyce/java/elements/toc.html