How do we know that diamond and graphite are different structures of carbon?

In the first part of this post, I explained how scientists found out in the late 18th century that diamond, graphite, and charcoal were all made of carbon.  As a quick explanation of how such different materials could be made of the same element, I put up the following photo, showing that diamond and graphite actually have vastly different structures:

It’s natural to wonder how we know that they’re made of the same element, but it’s also natural to wonder how we know that they have these exact structures.  I (hopefully) answered the first question in my earlier post.  This post is devoted to answering the second question:  how do we know that diamond and graphite are different structures of carbon?

The answer, as in so many science fiction movies, is radiation.  In this case, it’s x-ray radiation.  In a tangential kind of way, it almost makes sense that x-rays would be the answer:  after all, you use them to look inside things, so why wouldn’t they be good to look inside a solid crystal structure like a diamond or a chunk of graphite?  But we use x-rays to look into, e.g., the human body because human flesh is largely transparent to x-rays, much as a red-tinted window is largely transparent to red light (while blocking other colors of light).  In contrast, we get information from x-rays about materials like diamonds by bouncing the x-rays off of them.

How does that work?  Well, some of you might remember that x-rays are a form of light that is invisible to humans (much like UV rays or microwaves).  You might also remember that light behaves like a wave in certain situations.  One of the most important features of waves is their ability to interfere with one another.  When two waves meet, they add together to form a new wave.  This means that if their high points overlap, the new wave’s high point will be really high.  And if their low points overlap, the new wave’s low point will be really low:

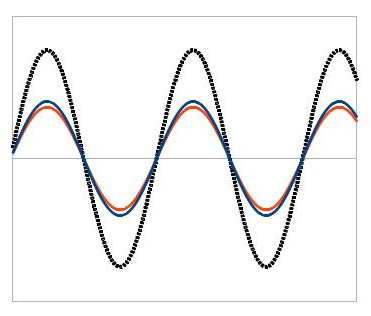
We call a situation like this constructive interference.  On the other hand, if one wave’s high point overlaps with the other wave’s low point, the new wave will be much lower:

 

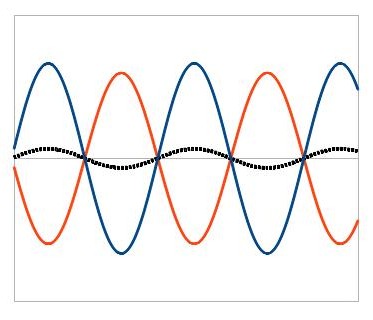
We call this destructive interference.  Constructive and destructive interference are the two extremes, but in a real situation where 2 waves overlap, generally you’ll have some parts that constructively interfere and some parts that destructively interfere, as well as some in between parts.  This causes a complicated pattern known as a diffraction pattern, sometimes called an interference pattern.

So what does all this have to do with the structure of diamonds and graphite?  Well, what we haven’t mentioned is that it’s possible to change how waves overlap and interfere with each other.  How do we do that?  One of the easiest ways is to have the waves follow slightly different paths, so that they no longer line up with one another.  Here’s a picture of one way this can happen:

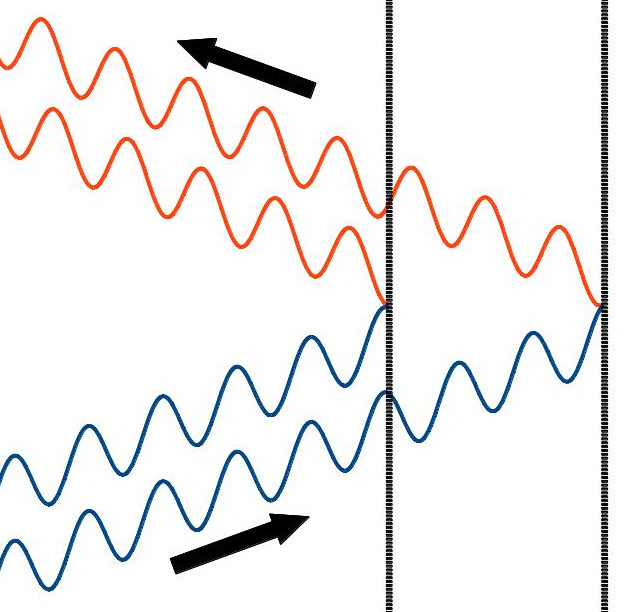In this picture, you have the blue waves coming in, part of them reflecting off the first barrier, and part of them passing through the first barrier and reflecting off the second barrier, and both coming back out as represented by the orange waves.  (Just real quickly:  the colors I’ve used have nothing to do with the colors of the light going into or out of this system.  I just chose different colors to emphasize which waves were incoming and which ones were outgoing).  One thing you may notice is that the blue waves are going to interfere constructively because they stack up on top of each other very nicely: crest to crest and trough to trough.  The orange waves, on the other hand, don’t stack up very nicely at all.  In other words, the blue waves constructively interfere and the orange waves destructively interfere.  That may be tough to see in the picture above, but if we add the blue waves together and then add the orange waves together, we get this:

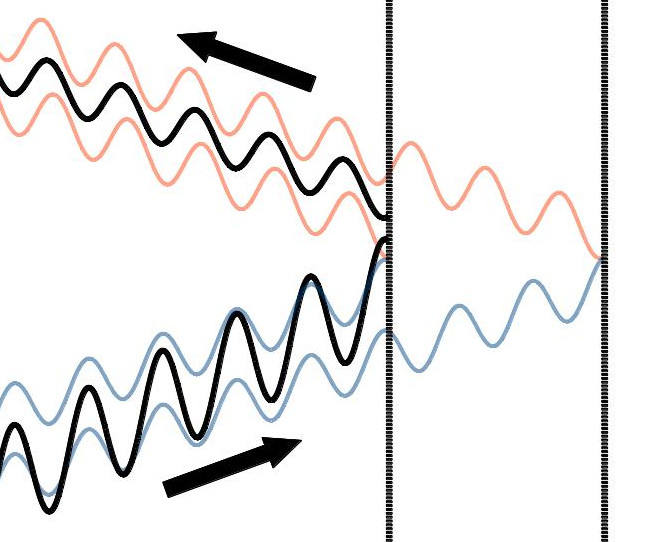So there’s a much smaller wave going out than there is coming in.  But why does this happen?  To answer that, we need a little vocabulary lesson:

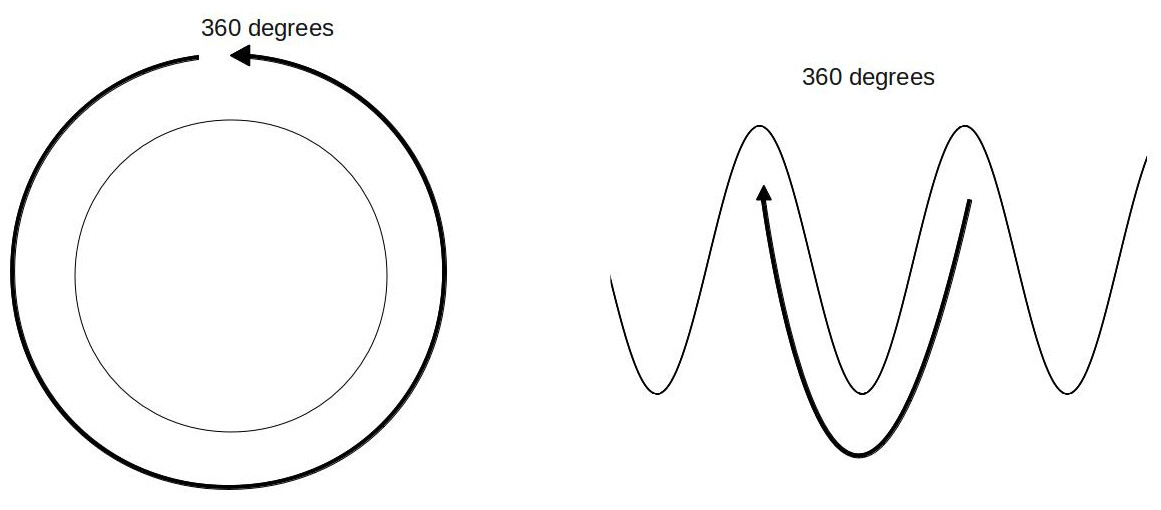
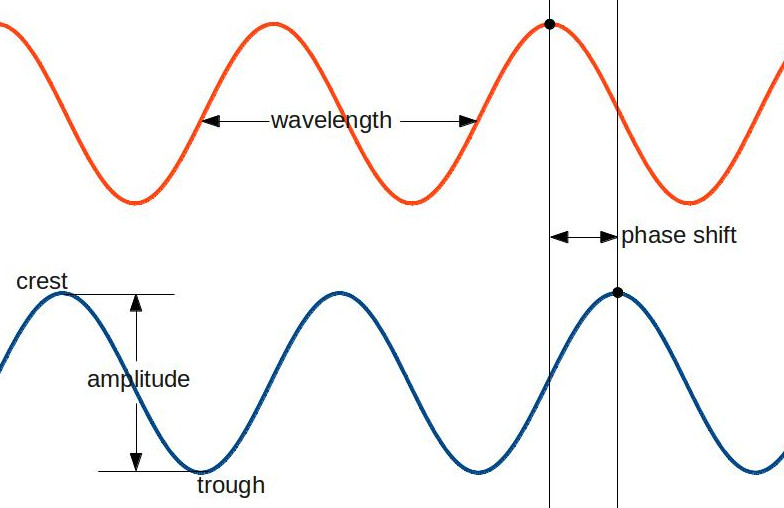These terms are all pretty standard among scientists.  The crest of a wave is its highest point, while the trough is its lowest.  The distance between crest and trough is the amplitude, and the distance from crest to crest, trough to trough, or between any two comparable points is called the wavelength.  If you have two waves (like the orange and blue ones above), then the distance between their crests (or their troughs, or any two comparable points) is called the phase shift.  Knowing this terminology will help in general, but what we’re really interested in is the phase shift between two waves.  That’s because it tells us whether the waves will interfere constructively or destructively.  The waves interfere most constructively when the crest of one is right on top of the crest of another.  That means that the phase shift in this case is zero.  The waves interfere most destructively when the crest of one wave overlaps with the trough of another wave.  We say that the phase shift is 180 degrees in this case (this terminology is just like what’s used for a circle, and the reason for that will become apparent soon).  One important thing to notice is that if we start with the waves overlapping (zero phase shift) and move them until one crest is above a trough (180 degrees phase shift), then if we keep moving them in the same direction, we will end up with the waves overlapping again (360 degrees).  The reason we use the circle terminology in this case might be a little easier to explain now.  If we start at the top of a circle and go 360 degrees, we end up at the same place as where we started.  Likewise, if we start at the crest of a wave and go through a 360-degree phase shift, we end up at an identical place on the wave, just shifted by one wavelength.  As a side note, systems that behave in this way, repeating themselves at regular intervals, are called periodic.

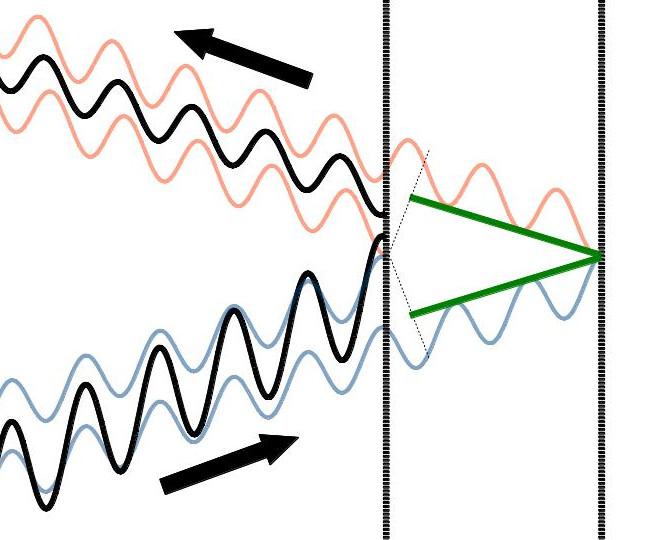
So let’s go back to the picture we had earlier of the light waves bouncing off a surface and interfering.  I’ve added two green lines to the picture:

These green lines represent the extra distance that the outer wave travels beyond the distance traveled by the inner wave.  (Aside:  the reason they don’t extend all the way from one surface to the other is because the outer waves are separated by a small distance from the inner waves).  It’s probably fairly easy to see that this distance gets longer as we open up the angle wider.  What might be more difficult to see is that, because this distance changes as the angle of the incoming light changes, the interference of the waves will change as well.  Why does this happen?

Well, think of it this way.  We know that the incoming waves are not phase shifted at all relative to one another.  That’s why they constructively interfere.  If they were both reflected from the first surface, they would continue to have the same phase shift, i.e., they would continue to constructively interfere.  But now let’s assume that the outer wave is reflected off the back surface and therefore now travels the extra distance represented by the green lines.  Now there may be a phase shift between the outer and inner waves, as we’ve shown in the pictures.  What if the extra distance traveled by the outer wave just happened to be one half of the wavelength of the wave?  Then, when the outer wave rejoined the inner wave on their outbound journey, they would be 180 degrees phase shifted from one another.  In other words, they would destructively interfere.  Then again, if the extra distance happened to be one full wavelength, then the waves would be 360 degrees phase shifted and would constructively interfere again.  This pattern would repeat over and over as the angle of incidence of the waves was increased.

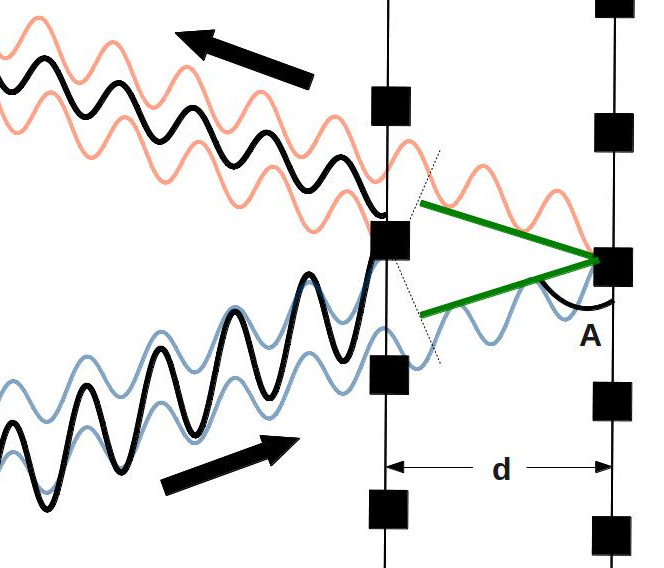
Believe it or not, this effect is a major piece of the puzzle of how we know that diamond and graphite are different structures of carbon.  The father-son team of William Henry and William Lawrence Bragg were working on this exact problem in the early 20th century.  We can see how the work we’ve done above is relevant to this question by making a few small changes to our picture above.

I’ve tried to show explicitly what the Braggs were thinking:  instead of waves reflecting off a barrier, here they’re reflecting off atoms (the big black squares) in a crystal.  The Braggs were using this picture to figure out how they could use x-ray waves to learn about the distance () between the atoms in a crystal.  They used the exact reasoning above to formulate an equation to explain how waves of x-rays would bounce off the atoms in a crystal.

We can actually work this equation out pretty easily.  We start with what we already know:  that the waves bouncing off a surface will only constructively interfere when the green lines in the picture are equal to a whole wavelength (or two whole wavelengths, or three, etc., but not a half a wavelength, since that would lead to destructive interference).  So we can make a crude equation out of this:

   

We’ll represent the wavelength using the Greek letter lambda, , which is the standard practice among scientists.  We can go ahead and call the whole number , for “number.”  So we have:

   

Now we just have to figure out how long the green lines are.  We do that by looking at a simplified diagram:

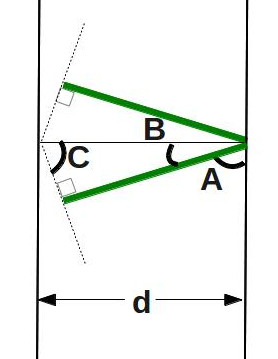This shows us that the green line makes a right triangle with the distance between the two planes of atoms.  We can use “soh cah toa” to figure out how long the green line is.  How?  First, we have to figure out what angle is.  We know that degrees, as it makes the corner of a rectangle.  We also know from last week’s post that the angles of a triangle add up to 180 degrees.  Since this is a right triangle, that means that , which, when we combine that with the result above, means that .  So now we can use some trigonometry (sine of an angle is opposite over hypotenuse) to get:

   

Plugging in the distance , and remembering that ,

   

So this means that one segment of the green line is going to be equal to .  Since there are two segments (one incoming and one outgoing), this means the extra distance that the outer wave travels is .  To get constructive interference, we know that this distance has to be a whole number multiplied by the wavelength of the wave, or in symbols:

   

This is what’s known as Bragg’s law, and it’s what the Braggs derived to figure out the distance between atoms in a crystal.  The great insight of the Braggs was that the wavelength of x-rays was roughly the same as the spacing between atoms in a crystal, so that they could look at the interference patterns produced at a bunch of different angles and get an idea of how far each atom in the crystal was from every other atom.  In 1913, they decided to bounce x-rays off a diamond and record the diffraction pattern.  This is a scan of William Lawrence Bragg’s actual notebook from the first experiment:

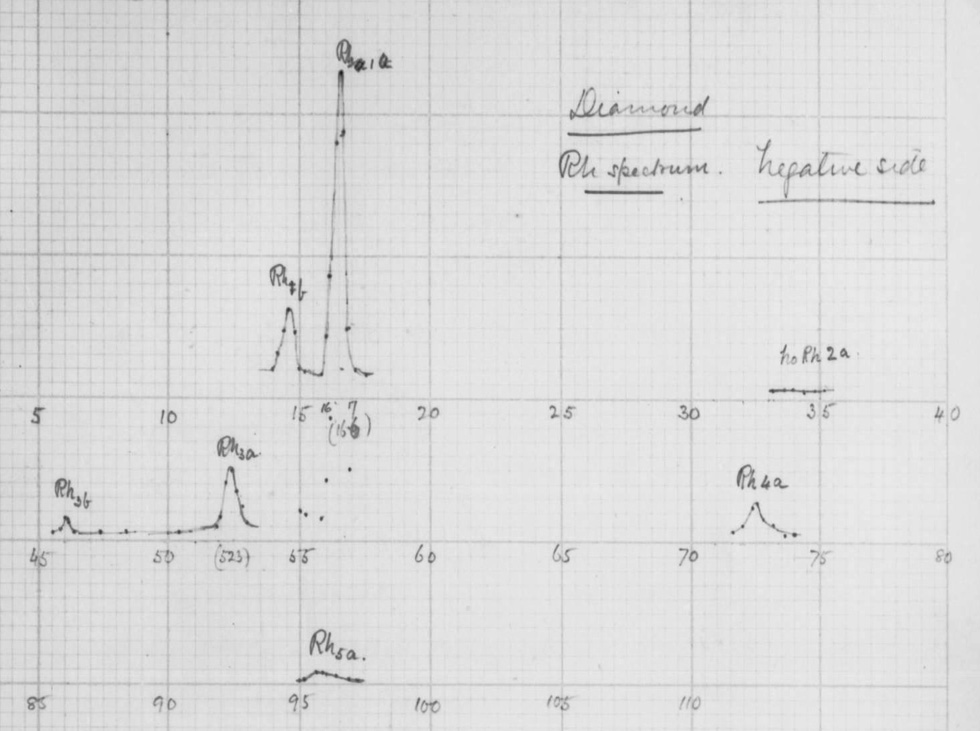
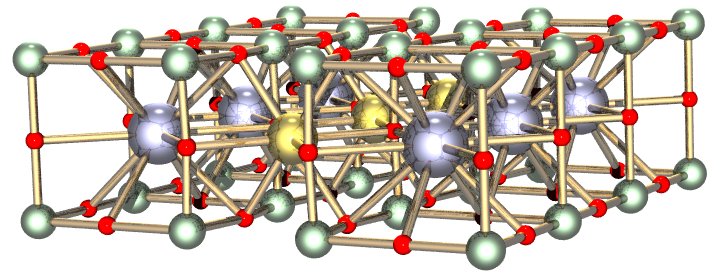
The peaks that are recorded here represent the constructive interference that the Braggs observed at various angles.  With these peaks and using the law that they derived, the Braggs could determine the distance between carbon atoms in diamond.  What they finally came up with was the picture at the top of this post.  A decade later, in 1924, J. D. Bernal would solve the structure of graphite using the same x-ray technique.  The Braggs would receive the 1915 Nobel Prize in Physics for their use of x-rays to elucidate the structure of matter, and their technique, now called x-ray diffraction or x-ray crystallography, is still used to this day to figure out the structure of everything from biological molecules to superconductors and everything in between.  Here are a few examples of the structures that have been figured out.  This is the superconductor known as YBCO:

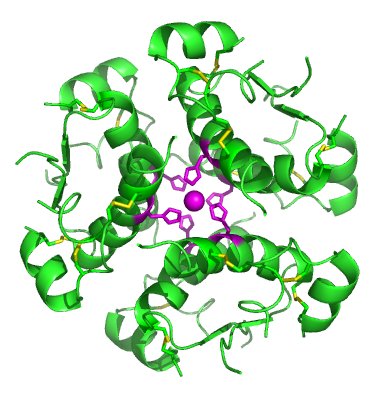
And here’s the x-ray structure of insulin:

And here’s probably the most famous diffraction pattern in history:

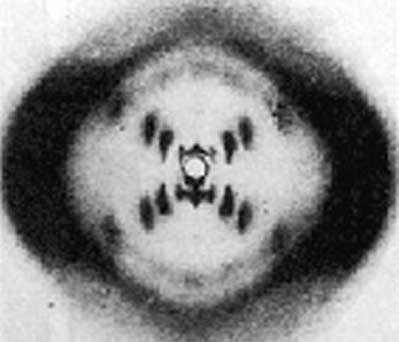This image, of purified DNA, was taken by Rosalind Franklin in 1952, and the pattern was solved by Franklin, Maurice Wilkins, James Watson, and Francis Crick to give the familiar double helix structure of DNA taught to every elementary school student today.  So not only did the Braggs’ technique answer the question of how we know that diamond and graphite are different structures, but it also eventually led to how we know that DNA is a double helix. X-ray crystallography is one of the most powerful and important tools in all of science.  If you ask the question, “How do we know what the structure of (insert substance here) is?” chances are the answer involves x-ray crystallography somehow.  And since the structure of matter is tied intimately to its function, in many cases, knowing the x-ray structure gives us hints about a substance’s behavior as well. It certainly gives us insight into how one element, carbon, can produce such different substances as diamond and graphite.

References

• The University of Leeds has archives of the Braggs’ notebooks from the period when they began to explore the structures of various crystals with x-rays.  The archives can be found here: http://www.leeds.ac.uk/library/spcoll/bragg-notebook/index.htm