How do we know that sin²&#952+cos²&#952=1?

I’m already late for this week’s post and I’m nowhere near done with the one I intended to post. So here’s a really quick post for the time being. You can probably already answer it yourself if you think a little bit about it. The equation $sin^2\theta+cos^2\theta=1$ may or may not be familiar to you from geometry or trigonometry, but it’s dead easy to prove. We use good old “soh cah toa.” For those of you scratching your heads in bemusement at this point, soh cah toa is a mnemonic for “sine is opposite over hypotenuse, cosine is adjacent over hypotenuse, tangent is opposite over adjacent.” A few of you may really be puzzled now. What I’m referring to is the definitions of the sine, cosine and tangent functions. They’re defined in terms of the lengths of the sides of a right triangle, as seen below:

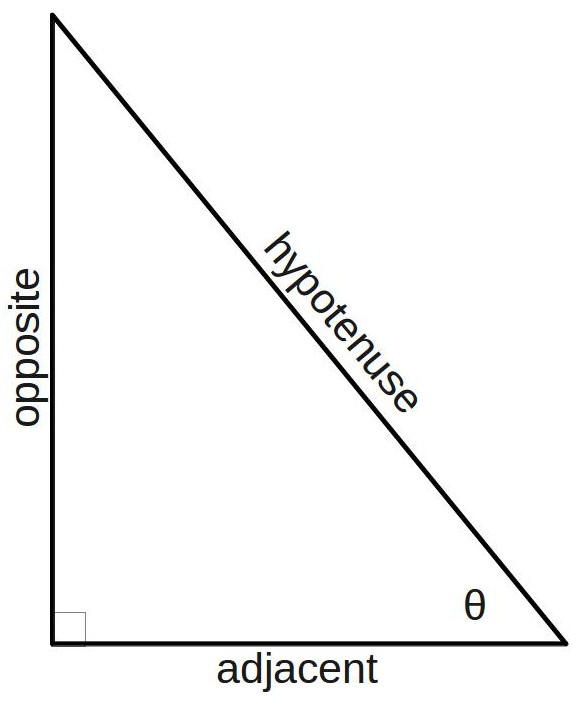As a refresher, a right triangle always has one angle equal to 90 degrees, and the side across from the 90-degree angle is known as the hypotenuse. Looking at the picture above, we can see the angle on the right side of the triangle labeled $\theta$ (pronounced theta), as well as the sides that are opposite and adjacent to $\theta$ and the hypotenuse. This lets us define the sine, cosine, and tangent, according to soh cah toa, as:

$sin\theta=\frac{\text{length of opposite side}}{\text{length of hypotenuse}}$

$cos\theta=\frac{\text{length of adjacent side}}{\text{length of hypotenuse}}$

$tan\theta=\frac{\text{length of opposite side}}{\text{length of adjacent side}}$

These definitions let us get a better handle on what we mean when we say $sin^2\theta+cos^2\theta=1$ :

$sin^2\theta=\frac{\text{opposite}^{2}}{\text{hypotenuse}^{2}}$

$cos^2\theta=\frac{\text{adjacent}^{2}}{\text{hypotenuse}^{2}}$

So this means that:

$sin^2\theta+cos^2\theta=\frac{\text{opposite}^{2}}{\text{hypotenuse}^{2}}+\frac{\text{adjacent}^{2}}{\text{hypotenuse}^{2}}=1$

We’ve set the whole thing to 1, because that’s what we learned in geometry class a million years ago. But let’s take a look at the second part of the equation above:

$\frac{\text{opposite}^{2}}{\text{hypotenuse}^{2}}+\frac{\text{adjacent}^{2}}{\text{hypotenuse}^{2}}=1$

If we multiply both sides through by the square of the hypotenuse, we get:

$\text{opposite}^{2}+\text{adjacent}^{2}=\text{hypotenuse}^{2}$

If that doesn’t sound familiar, then maybe you should go back and watch The Wizard of Oz, specifically the part where the scarecrow gets a brain. He says, “The sum of the square roots of any two sides of an isosceles triangle is equal to the square root of the remaining side.” Sound familiar now? It’s the Pythagorean theorem: $a^2+b^2=c^2$ . (Minor gripe: the scarecrow gets it all wrong: it’s only true for right triangles, not for isosceles triangles. And also only for squares of sides, not square roots. The Simpsons made fun of this in the episode, “$pringfield”).

You might be tempted to ask, “But Keith, how do we know that the Pythagorean theorem is true?” I could write a whole post just on that; there are hundreds of different ways to prove the Pythagorean theorem. But I’ll just leave you with one. It’s my favorite; it’s the first one I learned and it’s one of the easiest to remember that I know. It’s also quite pretty. We start with the picture below:

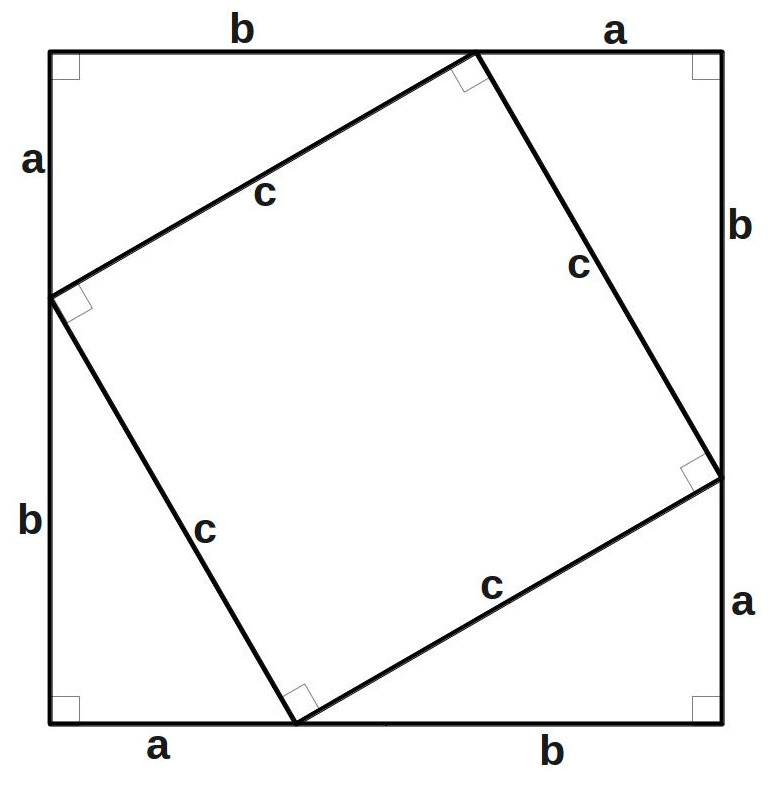This is just a picture of a small square tilted inside a big square. The small square has all of its sides equal to length $c$ , and the big square has sides equal to length $a+b$ . You might also notice that the small square divides up the big square such that there are 4 right triangles with sides $a$ and $b$ along the outside of the diagram. Our task now is to start calculating areas. The area of the small square is easy enough: $c^2$ . It’s right there in the name. For once, English and math aren’t on completely different wavelengths. The area of the big square isn’t too hard, either: $(a+b)^2$ . We can use the distributive property (or the FOIL method, if you learned it that way) to figure this out: $(a+b)^2=(a+b)(a+b)=a^2+2ab+b^2$ . In fact, we’ve already shown how we know the distributive property works in another post (HDWKI?).

So now we have the area of the small square: $c^2$ , and the area of the big square: $a^2+2ab+b^2$ . But we can also figure out the area of the small square by starting with the big square and chopping off those 4 triangles in the corners. We might remember that the area of a triangle is half its base times its height. Well, in this case, the base of each triangle is $a$ and the height is $b$ . This means the area of the triangle is $A_{\Delta}=\frac{1}{2}ab$ . Since there are 4 triangles, the total area of all the triangles is $2ab$ . But now when we start with the big square and chop off those 4 triangles, we get $a^2+2ab+b^2-2ab=a^2+b^2$ . But we chopped off those 4 triangles, so all we’re left with is the small square in the middle. That means that $a^2+b^2=c^2$ . But that means that we’ve proved the Pythagorean theorem and we’re done.