How do we know that light is a particle?

If you’re reading this blog, you probably have a passing familiarity with the word “photon,” even if it’s only in reference to the torpedoes that arm most of the Federation ships on Star Trek.  But just in case you chose to spend your teenage years enjoying sunlight and people that exist in real life, a photon is the smallest possible particle of light that you can have.  “But Keith,” you say, “I thought you just said that light is a wave.  Now you’re telling me it’s a particle.  Most of your arguments in the last post about light had to do with showing how light can’t be a particle.  It can spread out, interfere with itself, bend around objects, remember?”  Yes, I remember.  I was hoping you wouldn’t notice.  I guess I’ll have to try to distract you by changing topics completely.  In a previous HDWKI, we discussed the Doppler effect as a way to find planets orbiting other stars.  In it, we mentioned briefly that blue light and red light have different energies, and that blue light is more energetic than red light.  Actually, it’s a long-established fact that the shorter the wavelength of light, the more energy the light contains.  And you’re probably asking right now:  “What does any of this have to do with light being a particle?  And, come to think of it, how do we know that shorter wavelengths of light are more energetic, anyway?”  I would tell you to stop asking questions faster than I can answer them, but in this case, the answers to the two questions are related in a pretty unexpected way.

Maxwell and the “End of Physics”

Okay, so I kind of fibbed when I said before that it’s a long-established fact that shorter wavelengths of light contain more energy.  Until the 20th century, no one really thought the color of the light had anything at all to do with its energy.  Naturally, people thought the main factor was the light’s intensity.  Basically, the brighter the light, the more energy it has.  This totally makes sense.  And it’s true; brighter lights require more juice:  just try powering the Bat signal with a few AAA batteries.  In fact, a Scottish physicist named James Clerk Maxwell basically codified this intuition into physical law in the mid-1800s, when he formulated his Victorian-era Theory of Everything in a handful of equations.  Maxwell’s equations, as they’re now imaginatively called, combined electricity and magnetism and showed that light was just made up of waves of both.  They also predicted that the energy of a beam of light is only determined by its brightness, and is in no way related to its color.  Maxwell’s theory also happened to be one of the most successful theories up to that point in history.  Combined with the brand-new laws of thermodynamics and a few reformulations of the mechanical laws first introduced by Newton, it looked as if physics were nearing its endgame.  Lord Kelvin is alleged to have exclaimed, “There is nothing new to be discovered in physics now,” perhaps vying to get his picture in the dictionary next to the word “hubris.”  But it is remarkable that, even today, Maxwell’s equations explain almost everything that there is to observe about light and its interactions with matter.

Almost:  the most exciting word in physics.

Scientists nowadays divide the history of physics into two eras.  “Classical” physics is the era starting with the discoveries of Newton and Galileo in the 17th century, running all the way up through Maxwell’s work on light and electromagnetism, and ending in 1900.  “Modern” physics refers to developments after 1900, and includes Einstein’s relativity as well as quantum mechanics.  Einstein’s papers on special relativity weren’t published until 1905, though.  So what happened in 1900?  It turns out that there was one perfectly ordinary, everyday phenomenon that classical physics was at an utter loss to explain.  However, by making a small tweak to the mathematics describing the phenomenon, a German physicist named Max Planck arrived at a model that correctly described its behavior.  As luck would have it, this small tweak so fundamentally altered the way that scientists view the world that it almost single-handedly ushered in the modern era of physics.  But I’m getting ahead of myself.  What was the phenomenon that Planck was working on?  And what was his tweak?  And what does this have to do with light being a particle?

What is fire and why does it glow?

Planck was working on a problem known as blackbody radiation, which was first proposed in its full form by Gustav Kirchoff in 1860.  In a nutshell, the problem attempts to explain the observation that objects glow when they’re heated up.  Furthermore, as an object is heated to higher and higher temperatures, the color of this glow changes from red to orange to yellow and finally to brilliant white.  We are all familiar with the coil on an electric stove, which glows a dull red to orange color when set on high–the coil can reach temperatures of 750°C (about 1400°F).  But there’s an even more primitive example that we know of.  In a fire, a chemical reaction (usually between oxygen and some combustible material) occurs that generates gases, microscopic soot particles, and a lot of heat.  In fact, the reaction generates so much heat that the soot particles literally glow white hot.  We call this glowing material a flame.  A typical candle flame can be between 1000°C and 1500°C (about 1800-2700°F).  As the soot particles move higher–and further from the active chemical reaction–they begin to cool and the color of light they emit changes from white to orange to red before finally disappearing.  This is clearly visible in the picture below.

Planck’s goal was to find out how exactly matter, heat, and light were related.  This involved putting together ideas from a number of different areas of physics:

1) An object’s temperature is related to how fast its atoms and molecules are moving, with faster moving molecules corresponding to a hotter object, something we discussed in a post long ago.

2) All matter is made of particles that are electrically charged.  This theory was, in fact, quite young during Planck’s lifetime.

3) Maxwell’s equations tell us that if you wiggle an electrically charged object back and forth, you produce electromagnetic waves–a fancy term for “light”–and the color of this light corresponds to how quickly you wiggle the electric charge.

From these three pieces of information, we can put together a reasonably accurate picture of what is going on in a glowing heated object:  Basically, when an object is heated, some of its electrically charged particles (which we know now to be electrons) start wiggling.  This wiggling causes them to generate light.  As they are heated more and more, they wiggle faster and faster, generating light with different color (increasing frequency, or, as we have discussed before, decreasing wavelength).  A glowing object, then, is an object whose electrically charged particles have been heated to the point that they’re wiggling enough to create visible light.

The reverse case also happens.  Light is composed of waves of electric and magnetic fields.  Just as wiggling electric charges generate light waves, the light waves themselves can wiggle and jiggle electric charges.  This is an important point:  when wiggling charges generate light, we say that the object emits light.  Likewise, when light waves wiggle electric charges in a body, we say that the object absorbs light.  In fact, because energy is conserved, we can conclude that a wiggling charge that emits a light wave will wiggle less, because some of its energy of motion has escaped as light.  Conversely, a light wave that wiggles a charge will become a less intense light wave, since it has lost some of its energy to setting the charge in motion.

Planck’s “small tweak”

The theory mentioned above was not invented by Planck.  In fact, in Planck’s day, classical physics already had all of the mathematical machinery needed to calculate the behavior of glowing hot objects.  But what, exactly, was the behavior of these objects?  As we have mentioned above, heated objects glow with a certain color.  But they aren’t just one color; they’re a whole spectrum, just as white light from the sun is shown to be a spectrum consisting of all the colors of the rainbow.

Planck and his contemporaries were interested in calculating the spectrum of this “blackbody radiation.”  In fact, one of Planck’s colleagues, Willy Wien (a strong contender for “world’s silliest name”), had a considerable degree of success calculating the spectrum of blackbody radiation for short wavelengths.  Across the channel, Lord Rayleigh was able to calculate the spectrum for longer wavelengths.  However, a pair of experimentalists, Lummer and Pringsheim, performed detailed measurements of blackbody radiation and showed that neither Rayleigh’s formula nor Wien’s formula adequately fit the experimental data.

What happened next was kind of messy from an historical viewpoint.  It’s well-known that Planck was familiar with Wien’s work, but at some point he also became aware of Rayleigh’s work, even though he didn’t acknowledge it in his papers.  Planck used both formulas to stitch together an equation which seemed to accurately describe the measurements obtained by Lummer and Pringsheim.  However, in his initial paper, Planck merely gave the equation without proof.  He still needed to derive his equation from first principles.

Planck used Wien’s earlier work as a starting point.  Since the light emitted by an object has a certain spectrum, it’s made up of waves with many different wavelengths.  If these light waves are exchanging energy with the wiggling electric charges in an object (Planck called them “resonators”), then the resonators will wiggle at many different rates, or frequencies.  Wien and Planck both assumed that the energy of a resonator was determined by its amplitude (amplitude can be thought of as roughly how far the resonators travel when they’re wiggling.  We’ve used the term before with respect to the amplitude of light waves).  Both of them also assumed that it was possible for a resonator to wiggle at any frequency at all.  However, Wien further assumed that it was possible for a resonator to wiggle with any amplitude as well.  But Planck realized that, in order for the math to work out so that he could derive his blackbody equation, he had to drop Wien’s assumption that resonators could wiggle with any arbitrary amplitude.  In fact, he had to assume that they could only wiggle with very specific amplitudes.  He expressed this mathematically with the following equation:

   

Here, is the total energy of a resonator, is a whole number (1, 2, 3 …), and is a tiny unit of energy.  So if a resonator was wiggling at all, Planck’s work stated that it could only have an energy of , , , etc., but that it couldn’t have , or , etc.  Einstein (whose work we’ll talk about in the next section) came up with a clever name for these energy units.  He called them quanta.  With a small tweak to Wien’s blackbody math, Planck had unwittingly invented quantum mechanics.

Einstein earns his Nobel Prize

I used the term “unwittingly” deliberately.  By Planck’s own admission, he was simply making the assumptions he needed to make in order to get his blackbody formula to work. But he did contribute one other vital piece of information.  See, Planck decided to consider the thermodynamics of the resonators, and by reexamining Wien’s work, he was able to show that one of the thermodynamic quantities (entropy, for those who are curious) obeys a simple equation which depends on the frequency of the resonator.  However, because his resonators only wiggle in whole-number units, it turns out that the entropy depends on energy in the exact same way as it depends on frequency.  This means that the energy and the frequency of the resonators have to be directly related:

   

Here as before, refers to a single quantum of energy, refers to the frequency of the resonator, and is a new physical constant, known to us today as Planck’s constant.  The value of gives us the size of a single quantum of energy for a given frequency.  Its value is approximately:

0.0000000000000000000000000000000006626 J·s

This is a tiny number, and it illustrates why classical physics held sway for so long.  We know now that the quantum world is grainy, but the grains are so small that they’re easy to miss.

It turns out that is the whole reason we know that light is made up of particles.  But it wasn’t Planck who realized this.  No, it would take some sort of Einstein to figure out something that crazy.

Luckily for us, Albert Einstein was some sort of Einstein.  He was familiar with the paper that Planck had written in 1900 introducing the concept of a quantum (something we now call energy quantization).  But, whereas Planck had seen energy quantization as a mere mathematical convenience, Einstein considered the possibility that quanta are real physical objects.  In particular, Einstein was interested in the application of Planck’s quantum theory to an observation known as the photoelectric effect.  The photoelectric effect was discovered by Heinrich Hertz in 1887.  He was working on an experimental apparatus that looked a lot like the spark plugs in your car, trying to determine how sparks of electricity are created.  Hertz noticed that when he shined ultraviolet (UV) light onto the apparatus, he could produce a spark.  In the ensuing 15 years, scientists were able to show that the spark was the result of UV light knocking electrons out of the metal coils in Hertz’s “spark plug.”  In 1902, a Hungarian named Philipp Lenard made a breakthrough.  He noticed that there was a threshold minimum frequency of light that was required to knock electrons out of a material.  This means, for example, that if you shine blue light on a chunk of sodium metal, you’ll knock electrons loose, but if you shine red light on it (since red light has a lower frequency than blue light), you won’t.

Remember at this point that according to Maxwell, the energy of the incoming light was determined only by its intensity.  But the photoelectric effect directly contradicts this.  No matter how bright your red light is, you won’t knock any electrons out of the sodium metal.  But shine even a weak blue light on it, and immediately, it starts to release electrons:

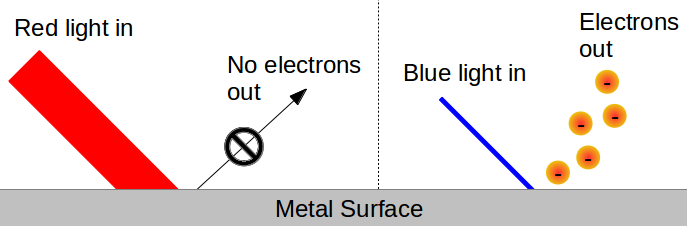Even more striking, once the frequency of the light is higher than the threshold, the number of electrons that are knocked loose from the metal isrelated to the light’s intensity, and onlythe intensity. From the perspective of classical physics, this is really weird.  However, Einstein saw that Planck’s equation clearly predicted that the energy of light is directly related to its color.  Moreover, Planck’s other equation predicted that the energy of the light is delivered to the metal in a discrete number of little packets.  Einstein made the connection with the little packets of light going into the metal and the other little packets–the electrons–coming out of the metal and put forward a bold idea.  In Einstein’s words (translated from German by Wikisource):

According to this picture, the energy of a light wave emitted from a point source is not spread continuously over ever larger volumes, but consists of a finite number of energy quanta that are spatially localized at points of space, move without dividing and are absorbed or generated only as a whole.

In other words, light is made up of a stream of particles–which nowadays we call photons.  To explain the photoelectric effect, Einstein reasoned that in order to knock an electron out of a piece of metal, each photon has to do a threshold amount of work (in fact, modern scientists call this the work function of the metal and refer to it with the Greek symbol ).  If an individual photon’s energy, measured from its frequency by the equation , is less than the work function , then the individual photon does not have enough energy to knock the electron out of the metal.  However, if the photon’s energy is more than the work function, , then the photon can knock an electron loose from the metal.  And furthermore, the energy of the electron coming out of the metal (as measured by the electron’s speed) will be equal to whatever energy the photon has left over after it’s knocked the electron loose:

   

An American named Robert Andrews Millikan undertook an extensive study of the photoelectric effect, and published papers in 1914 and 1916 confirming all of the  predictions from Einstein’s 1905 paper.  Einstein did a lot for science in his life:  special and general relativity, mass-energy equivalence, Brownian motion, quantum statistics, the list goes on and on.  But this breakthrough, the thought that light was made of discrete packets of energy, was what would eventually win Einstein his Nobel Prize in 1921.

Compton and final confirmation of the photon

Einstein’s introduction of photons and his realistic concept of quanta found their way into scientific discourse fairly readily, as many young scientists in the early 20th century began to adopt quantum theory to explain a whole host of atomic and molecular phenomena.  Of course, there was skepticism; there’s no way you can advance a theory that overturns the last 400 years of scientific progress without at least a little bit of pushback.  Most of the older physicists (like Wien and, surprisingly, Planck himself) refused to believe that quanta and photons were real physical objects.  They thought that quantum theory was a mathematical convenience:  the formulas correctly described the experiments, but only because they were approximations to a reality that aligned itself more with Maxwell’s classical physics than Planck’s and Einstein’s quantum physics.

In 1923, Arthur Compton, a scientist at Washington University in St. Louis, put the final puzzle piece in place to confirm the existence of the photon.  His basic experiment was to show that when light (in this case, X-rays) is shined on an electron, the light particle and electron bounce off of each other, obeying the conservation of energy.  The key observation that Compton made was that the frequency (color) of the light changed when it bounced off an electron.  Using Planck’s law, Compton showed that the change in frequency was exactly compensated by the recoil in the electron, an observation that couldn’t be explained with Maxwell’s laws and classical physics.  Compton had shown that discrete bundles of light exchange energy as well as momentum with electrons, and that the quantum description of light as a particle, a photon, had to be true.

This has been a long post, but the introduction of the modern theory of the photon is one of the most important moments in the history of physics.  Of the scientists listed in this post, Wien, Planck, Einstein, Millikan, and Compton all won Nobel Prizes for their work, as did many others working in this field whom I have failed to mention (but I’m hoping I can come back to them in one, or more, future HDWKI’s).  I’ve left a lot of open questions.  I’ll send you off with one:  the work described here shows that light behaves as a particle.  But the work in the last post on this topic shows that light behaves as a wave.  So which is it?  Stay tuned for a future HDWKI.

References

Some wonderful soul (I think it was Koji Ando) has done a brilliant job translating Planck’s original paper from German to English and has made it available here:

• http://people.isy.liu.se/jalar/kurser/QF/references/Planck1901.pdf

Wien’s papers, on the other hand, are much more difficult to track down.  Here’s a website with links to a bunch of them in their original German.

• http://de.wikisource.org/wiki/Wilhelm_Wien

Einstein’s 1905 paper introducing the concept of the photon (translated to English):

• http://en.wikisource.org/wiki/On_a_Heuristic_Point_of_View_about_the_Creation_and_Conversion_of_Light

Millikan’s 1914 paper (paywalled):

• http://prola.aps.org/abstract/PR/v4/i1/p73_2

Compton’s 1923 paper (paywalled):

• http://prola.aps.org/abstract/PR/v21/i5/p483_1