Category: Mathematics

How do we know that sin²&#952+cos²&#952=1?

Post author By Keith
Post date May 9, 2013
1 Comment on How do we know that sin²&#952+cos²&#952=1?

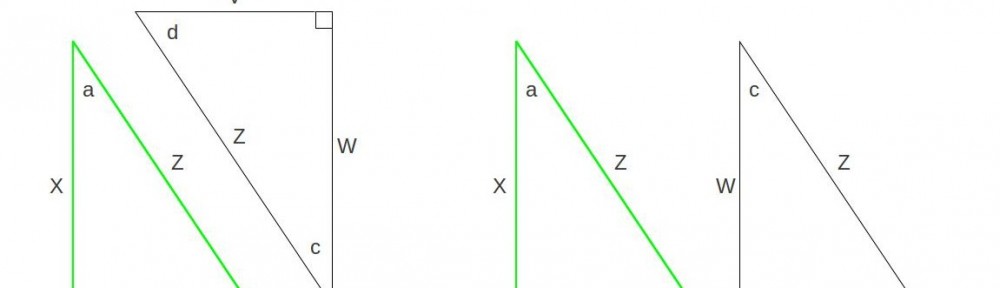
I’m already late for this week’s post and I’m nowhere near done with the one I intended to post. So here’s a really quick post for the time being. You can probably already answer it yourself if you think a little bit about it. The equation $sin^2\theta+cos^2\theta=1$ may or may not be familiar to you from geometry or trigonometry, but it’s dead easy to prove. We use good old “soh cah toa.” For those of you scratching your heads in bemusement at this point, soh cah toa is a mnemonic for “sine is opposite over hypotenuse, cosine is adjacent over hypotenuse, tangent is opposite over adjacent.” A few of you may really be puzzled now. What I’m referring to is the definitions of the sine, cosine and tangent functions. They’re defined in terms of the lengths of the sides of a right triangle, as seen below:

Tags Geometry, Math, Pythagorean theorem, Trigonometry

Mathematics

How do we know that the angles of a triangle add up to 180 degrees?

Post author By Keith
Post date April 22, 2013
No Comments on How do we know that the angles of a triangle add up to 180 degrees?

I know I promised last time that I’d explain how we know about the different structures of diamond and graphite, but that one’s not quite ready yet. Plus, the last post was really long, so I figured I’d give your brain a little rest and do some high-school geometry (some of you might not consider that a “rest,” but I promise to make it as painless as I can). The fact that you can unfold a triangle to make a straight line (180 degrees) has been known since ancient times, and it’s been the subject of some really ingenious proofs and some fundamental advances in math over the years. I wanted to take a moment to present you with two proofs: one that I just made up on the fly, and one from Euclid. The proofs are neat, and they give some insight into how mathematicians think about problems; but more importantly, I’ve got a couple of other HDWKI’s planned that will use some of these properties of triangles, so it helps to have a decent understanding of them now, so those posts don’t stretch on to eternity.

Tags Geometry, Math, Trigonometry

Mathematics

How do we know that 3×4 = 4×3 ?

Post author By Keith
Post date December 29, 2012
No Comments on How do we know that 3×4 = 4×3 ?

Why even ask a question like that? Everyone knows that $3\times4=4\times3$ , just like everyone knows that $3+4=4+3$ . Mathematicians would say that multiplication or addition of two numbers is commutative, meaning that you get the same answer regardless of the order in which you do the multiplication or addition. But what does that really mean? When we say $3\times4$ , we literally mean “3, 4 times,” or 4 sets of 3 objects each, or $3+3+3+3$ objects. Likewise, when we say $4\times3$ , we mean “4, 3 times,” or 3 sets of 4 objects each, or $4+4+4$ objects. Most people would think it’s obvious that $3\times4=4\times3$ , but it’s equivalent to saying that $3+3+3+3=4+4+4$ , which seems quite a bit less obvious. So how do we know it? Is the fact that multiplication is commutative just something we assume about numbers, or is there a way to prove it?