
“Well, that’s easy enough,” you might say. “Just take a spaceship, fly into outer space, and look back at the Earth. You’ll see that it’s clearly round.” That may be, but we’ve known the Earth is round for much longer than we’ve been able to go to space. So how long have we known that the Earth is round? And how did we know that it was round without being able to look at the planet from afar?
The Greeks
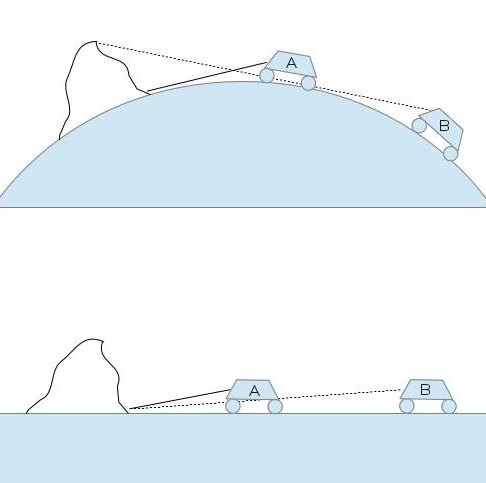
The earliest writings detailing the possibility of a round Earth come to us from the ancient Greeks. Starting in the 6th century BC, philosophers began putting together arguments in favor of a spherical Earth. Some of these arguments were based on unscientific assumptions; for example, one school, the Pythagoreans, believed that the sphere was the most perfect shape, so naturally the gods would choose to make the Earth a sphere. Other arguments were based on simple observations. For instance, when you observe a ship sailing toward the horizon, its hull appears to drop below the horizon before its mast. Similarly, if you’re a sailor on a ship moving toward land, the peaks of mountains and the tops of high buildings appear long before the coastline does. This phenomenon is familiar to anyone who’s driven west across the US. Upon approaching the Rocky Mountains, the snowcaps of the peaks are visible for miles before the bases of the mountains are.
Aristotle (384 BC-322 BC), in his work De Caelo, pointed out that there are stars that are high in the sky in some parts of the world and very close to the horizon (or even invisible) in other parts of the world. He also noted that the shadow of the Earth on the Moon during a lunar eclipse always appeared as the arc of a circle. A century or so later, Eratosthenes (c. 276 BC-c. 195 BC) was bold enough to attempt to calculate the circumference of the Earth by using the Sun’s position in the sky at various locations on the Earth’s surface. Another century later, Posidonius (c. 135 BC-51 BC) carried out a similar calculation, but using the position of a star (Canopus) in two different locations. After a few centuries, Ptolemy would revisit the Greeks’ arguments in his Almagest, which would become the authoritative text on astronomy for the next 1500 years until the time of Copernicus and Galileo.
How did Eratosthenes and Posidonius figure out the Earth’s size?
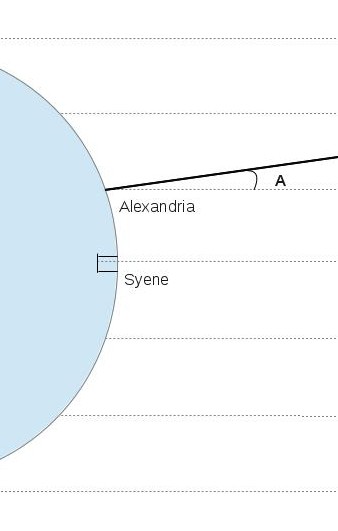
The methods of Eratosthenes and Posidonius are similar. We’ll cover how Eratosthenes made his determinations. First, he knew about a deep well in the Egyptian town of Syene (modern day Aswan). At noon on the summer solstice, it was known that the Sun shone down to the bottom of this well without casting a shadow. This meant that the Sun was directly overhead at Syene at this time of year.
Geodesy4Layman/80003002.GIF (public domain)
Eratosthenes then measured the angle of the sun in the sky at this exact moment in his hometown of Alexandria, about 500 miles north of Syene. His measurements showed that, at noon on the summer solstice, the Sun was at an angle of roughly 7.2 degrees from the vertical in Alexandria. With this angle and the distance between Alexandria and Syene, Eratosthenes had a rough value for the curvature of the Earth: every 500 miles north of Syene you travel will cause the Sun to be about 7.2 degrees lower in the sky at noon on the summer solstice. Eventually, if you keep going north, the Sun will be on the horizon. Continuing in the same direction (no longer called “north,” since by now you’ve passed the North Pole) will drop the Sun below the horizon. If you insist on continuing your journey, at some point the Sun will rise from the opposite side of where it originally dipped below the horizon. The question Eratosthenes wanted to answer was, “How far do you have to travel before the Sun is right back overhead?” It turns out that 7.2 degrees was a pretty convenient number, as it is equal to 1/50th of a circle: a full circle is 360 degrees, so 360 ÷ 7.2 = 50. So if traveling 500 miles changes the sun’s position by 1/50th of a circle (7.2 degrees), then in order to go a full circle, you’d have to travel 500 miles × 50 = 25,000 miles. And there you have it. Eratosthenes calculated the Earth’s circumference to be somewhere around 25,000 miles. How good was his calculation? Well, modern-day values pin the average circumference of the Earth at 24,901 miles, which means that Eratosthenes was accurate to within a half a percent.
The Muslims
Medieval Muslim astronomers were able to refine the measurements of Eratosthenes and Posidonious using various techniques. The most striking example is the work of Abu Rayhan al-Biruni, who in the 11th century made measurements of the Earth’s radius to within 20 km of its presently accepted value. How did Biruni improve upon the measurements of the ancient Greeks? He went to the top of a mountain and sited the angle of the horizon from this point. This information, coupled with the height of the mountain, gave him the radius of the Earth.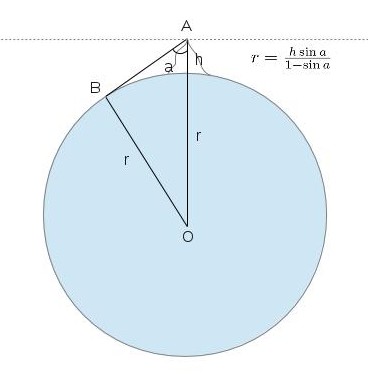
The figure on the right shows how Biruni was able to do this calculation. He measured the angle a that a plumb line at the top of the mountain made with the horizon. Since the line of sight AB is a line to the horizon, it is tangent to the Earth’s surface, which means that the angle OBA is a right angle. Biruni was able to use the sine function and a little bit of algebra to obtain the formula for the Earth’s radius r shown in the figure.
From the Age of Discovery to the Space Age
Later, as European explorers began making expeditions to the New World, Ferdinand Magellan would embark on his circumnavigation of the globe, a feat that would take over 3 years to complete and that would ultimately claim Magellan’s life in the process. Finally, in the 20th century, astronauts were able to take spaceships into outer space, look back on the Earth, and observe directly its spherical shape. And that’s how we know the Earth is round.
References
-
Posidonus, I. G. Kidd, Posidonius: Fragments: Volume 2, Commentary, Part 2, Cambridge University Press, pp. 720-722.
-
I. Fischer, “Another Look at Eratosthenes’ and Posidonius’ Determinations of the Earth’s Circumference,” Quarterly Journal of the Royal Astronomical Society, Vol. 16, p.152.
-
Aristotle, “On the Heavens,” Book II, Chapter 14, The Works of Aristotle, Oxford University Press; pp. 297-298.
-
B. Savizi, “Applicable problems in the history of mathematics: practical examples for the classroom,” Teaching Mathematics Applications, Vol. 26, pp. 45-50.

One reply on “How do we know the Earth is round?”
You should have elaborated more on the Posidonius measurement. Otherwise, this is a good article 🙂