How do we know how much stars weigh?

Note: I decided to take a short break from our story about the genetic code: to be honest, I’m a little biology-ed out right now. Don’t worry; I won’t leave you hanging for too long.

It seems like every time a story comes out in the news about astronomy, we always get descriptions like “a star with the mass 10 times that of the sun,” or “a planet with twice the mass of Jupiter.” In fact, it turns out that knowing the masses of stars, planets, galaxies, and black holes is critically important for testing our theories about dark matter, dark energy, and cosmology in general. But how do we figure out how massive these objects actually are? We can’t take a scale or a balance and go weigh them, like we can with objects on Earth. So how do we know it?

Newton’s Law of Gravity

The simplest way to figure out how much stars weigh is by watching pairs of stars. Just as we explained in our post on stars orbiting other planets, when two stars orbit one another, they tug on each other, causing a wobble that can be detected either visually or by the Doppler effect. Why does this work? Well, let’s take a look at Newton’s law of gravity:

$F=-\frac{Gm_{1}m_{2}}{r^2}$

This equation packs a lot of information into a tiny space, so we’ll break it into pieces to explain it. Let’s start by talking about the negative sign. In physics, we can have forces that push (like trying to push a piece of furniture into place) and forces that pull (like pulling open a drawer). In order to distinguish these types of forces, we just go ahead and arbitrarily say that a pushing force will always be positive (greater than zero), and a pulling force will always be negative (less than zero). This makes sense, because pushing is the opposite of pulling. If you use force to pull open a drawer, you can use the same amount of force in the opposite direction to push the drawer closed again. What this boils down to for Newton’s gravity is that the force of gravity, denoted by $F$ , is a pulling, or attractive, force. Gravity always attempts to pull objects together. It never pushes objects apart. This makes sense, too. Otherwise, we might fall up instead of down if the Earth’s gravity pushed us away from the ground instead of pulling us toward it.

So the negative sign just tells us the direction of the force. What we really want to know is how strong the force is, or its magnitude. We figure this out by looking at everything after the negative sign. $m_{1}$ and $m_{2}$ are masses of two objects exerting a gravitational force on each other. It’s pretty clear that if you make the masses bigger, the magnitude of the force (ignoring the negative sign) is going to get bigger. We say that the force of gravity is directly proportional to the masses of the objects involved. $r$ is the distance between the two objects. What happens if you make $r$ bigger? Well, you can plug in numbers to prove it for yourself, but as $r$ increases, $F$ gets closer to zero. And as $r$ decreases, the magnitude of $F$ gets bigger and bigger (again, ignoring the negative sign, since that just tells us whether the force is pulling or pushing). In words, this means that as two objects get closer together, the force of gravity between them gets stronger. We say that the force of gravity is inversely proportional to the distance between objects. (There’s actually a fascinating reason for why $F$ is inversely proportional to $r^2$ instead of just $r$ . It has to do with the fact that we live in a world where space is 3-dimensional. We’ll get to that in a future HDWKI.)

As a brief final note, we mention $G$ . $G$ is what’s known as a proportionality constant. It doesn’t change (at least as far as we know), and it tells us how strong the force of gravity is compared to other forces, like electric or magnetic forces. The most important thing about $G$ is that it’s small. Really small. This means that gravity is really really weak compared to other forces. This makes sense too. Think about the magnets on your fridge. You have the entire Earth pulling with all its gravity on these magnets, and yet they can easily stick to the fridge with just a little tiny bit of magnetic force. So gravity must be pretty darn weak compared to the magnetic force. (In fact, if you compare the gravitational force between two electrons and the electric force between them, you find that the electric force is around

$10,000,000,000,000,000,000,000,000,000,000,000,000,000,000$

times stronger than the gravitational force.)

Binary Stars

Ok, now we know how Newton’s law of gravity works. How do we use it to figure out how much stars weigh? Remember in our earlier post how we said an orbiting planet can make stars wobble? Well, this is because, even though the star is tugging on the planet with its gravity, the planet also tugs on the star with its own gravity. Some of you may be thinking, “This is like relativity: if you’re on the star, it looks like the planet’s orbiting you, but if you’re on the planet, it looks like the star’s orbiting you.” This works (kind of), but a better way to think about the situation in terms of Newton’s law is to realize that both the planet and the star are orbiting a point somewhere in between them.

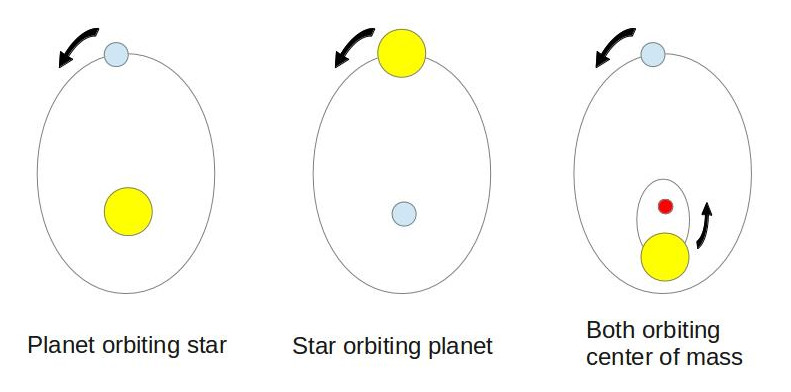The red point in the picture is called the center of mass. If you put the planet and star on opposite ends of a seesaw, the center of mass would be the point at which you would have to put the fulcrum for the star and planet to balance each other out. Amazingly, this seesaw analogy can work even in the case of stars and planets. Anyone who’s ever been on a seesaw can tell you that the heavier you are, the closer to the fulcrum you have to sit.

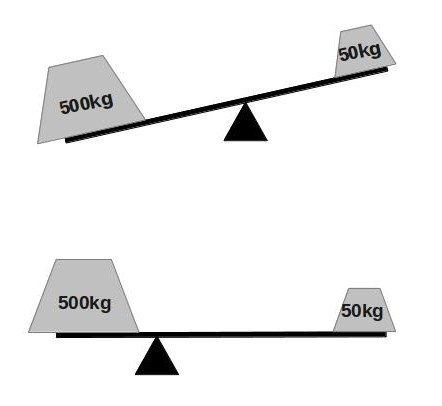You can balance the two sides of the seesaw if you move the fulcrum toward the heavier weight. How far do you have to move it? Well, let’s start by looking at what happens when you have two equal weights on the seesaw:

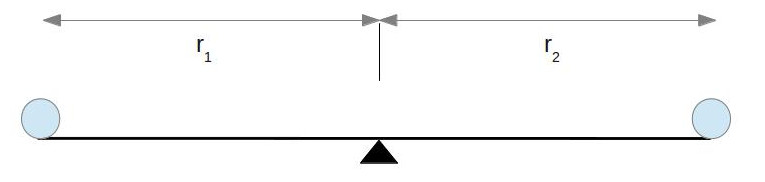It’s pretty obvious that if the balls weigh the same, then the balancing point of the seesaw will be right in the middle ( $r_{1}=r_{2}$ ). But now what happens if we double the weight on one side?

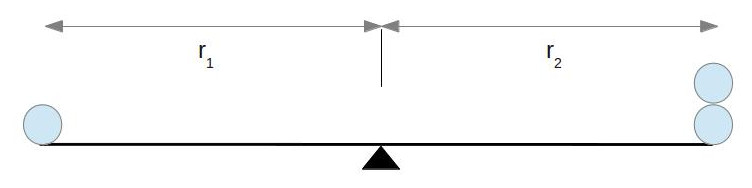Now there’s twice as much weight on the right side as on the left. Let’s call the amount of mass on the left $m_{1}$ and the mass on the right $m_{2}$ . We’ll need to move the balancing point to the right, decreasing $r_{2}$ . So this tells us that if we increase $m_{2}$ , we have to decrease $r_{2}$ to balance the fulcrum. There’s nothing special about the right side of the fulcrum, so the left side should behave the same way (if we increase $m_{1}$ , we have to decrease $r_{1}$ ). Just like in the case with gravity, this means that mass and distance are inversely proportional to one another:

$m_{1} \propto \frac{1}{r_{1}}$

$m_{2} \propto \frac{1}{r_{2}}$

where $\propto$ means “is proportional to.” (The term inversely proportional just means that mass $m$ is proportional to the inverse of distance $r$ , as shown above.) We can do a neat little trick by multiplying through by distance to get:

$m_{1}r_{1} \propto 1$

$m_{2}r_{2} \propto 1$

What does this mean? Well, since $m_{1}r_{1}$ and $m_{2}r_{2}$ are both proportional to 1, and 1 is a constant, that means that $m_{1}r_{1}$ and $m_{2}r_{2}$ are both going to be constants. I won’t get into the nitty gritty details here, but it turns out that they’re both equal to the same constant (call it $C$ ):

$m_{1}r_{1} = C$

$m_{2}r_{2} = C$

But that means they’re equal to each other!

$m_{1}r_{1} = m_{2}r_{2}$

or, to put it another way,

$\frac{m_{1}}{m_{2}}=\frac{r_{2}}{r_{1}}$

So if you know the ratio of the masses on either end of the seesaw, you can figure out the ratio of $r_{1}$ to $r_{2}$ , which will tell you where to put the balancing point. Notice also that this equation tells us that if we increase the mass of the object on the left side, we have to decrease $r_{1}$ , the distance between the mass on the left and the balancing point. In other words, we have to move the balancing point to the left, just as we expected.

What does this have to do with stars? It turns out that the exact same equation:

$\frac{m_{1}}{m_{2}}=\frac{r_{2}}{r_{1}}$

holds for two objects orbiting their center of mass. This equation is tough to use for a star-planet system, but it turns out to be great for a star-star system, or a binary star, as it’s called. This is because you can see both stars (usually through a telescope) and follow them over time to figure out their orbits. Once you know their orbits, you can find the common point that both of them are orbiting: their center of mass. Since you can see where everything is, you can measure the distance of each star to its center of mass. And if you know the distances, you can figure out what the ratio of the masses of the stars is to one another. So for binary stars, scientists use this seesaw method to figure out their masses.

What about single stars?

“But wait a sec, Keith,” you say. “The seesaw method only tells us the ratio of their masses. How do we know how much each one weighs individually? For that matter, what if the star we’re interested in doesn’t have another star orbiting it? How do we know how much that weighs?” This is a great question, and the cop-out answer is: we don’t really have a direct way of knowing the masses of individual stars. But we do have an interesting way of figuring out indirectly how much they weigh. How? By using stellar models. What’s a stellar model? In its most basic form, it’s an attempt to explain the behavior of a star. In a future HDWKI, we’ll tackle the question “How do we know what a star is?” For the moment, though, I’ll just describe a few of the things we know about stars and how we can use stellar models to figure out how much they weigh.

For starters, a star is basically a huge ball of really hot gas (mostly hydrogen and helium). This ball of gas is compressed together so tightly that there’s nuclear fusion going on at its center. That’s not terribly important right now. What is important is that you have two forces fighting each other: gravity, which wants to pull the gas tighter and tighter into itself (the end result of which would ultimately be a black hole); and the outward pressure of a continuous nuclear explosion at the core of the star, which wants to blow the star to smithereens. Miraculously, neither one of these forces wins (at least for the time being), and the star is in hydrostatic equilibrium, exactly balanced between gravity pulling inward and pressure pushing outward.

$F_{gravity}=F_{pressure}$

Another important piece of the puzzle is the brightness of the star, or its luminosity. If you heat anything, be it a coil on your stove, a piece of iron in a blacksmith’s forge, or even a giant ball of gas in space, it will start to glow and give off light. The more you heat it, the more light it gives off. In fact, there’s an equation to describe this situation:

$L \propto T^4$

This is known as the Stefan-Boltzmann law, after its discoverers. Basically, it says that the higher the temperature $T$ of the star, the more light it’ll give off–in other words, the higher its luminosity $L$ . (In an absolutely stunning turn of events, the reason why $L$ is proportional to $T^4$ , instead of just $T$ , has to do with the fact that we live in a world where space is 3-dimensional. Sometimes science is unabashedly mind-blowing.)

The next bit is tricky, so I’ll give an overview of the logic behind what we’re going to do before I get into the details. We start off with luminosity. We can figure out the luminosity of a star directly by observing it. We use the luminosity measurements to get a temperature for the star using the Stefan-Boltzmann law. We then use a stellar model to figure out how the temperature of the star relates to its pressure. Then we can use hydrostatic equilibrium to relate pressure to the force of gravity inside the star. Finally, we use Newton’s law to relate the force of gravity to the mass of the star.

Complicated enough? That’s fine; you can stop with that explanation if you’re satisfied. But if you want a little more, the math is below. But I warn you, I’m going to make it even more complicated by deriving all of it backward, so follow closely. Here we go:

We know from Newton’s law that the force of gravity is related to the mass and the radius of the star, and we know how they’re related:

$F_{gravity}=\frac{GM^2}{R^2}$

In this case, Newton’s law looks a little weird. Since the gravity from the ball of gas is acting on itself, we’ve just used $M$ as the mass for the whole ball, instead of $m_{1}$ and $m_{2}$ as separate masses. Ditto for $R$ : we’re using the radius of the star instead of a distance between two objects. We’ve also ignored the negative sign, as we know the magnitude of $F_{gravity}$ is going to have to equal the magnitude of $F_{pressure}$ for the system to be in equilibrium.

Now for the outgoing pressure. In physics, pressure is just defined as the amount of force over a given area:

$P=\frac{F}{A}$

This makes sense: for example, we inflate our tires to a pressure of 32 pounds per square inch. It’s just the force (in pounds) per area (square inches) that the air exerts on the insides of our tires. Moving on.

Now we assume that the star is a sphere. We know from geometry that the surface area of a sphere is $A=4\pi R^2$ . Plugging this into our equation for pressure:

$P=\frac{F_{pressure}}{4\pi R^2}$

But since we’re at equilibrium,

$F_{gravity}=F_{pressure}$

So combining the two equations:

$\begin{align*} P&=\frac{F_{pressure}}{4\pi R^2}\\ &=\frac{F_{gravity}}{4\pi R^2}\\ &=\frac{GM^2}{4\pi R^4} \end{align*}$

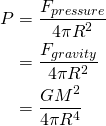
So now we know how the outward pressure is related to the mass and radius of the star. We can’t quite use this equation yet, but we can think about pressure in another way. We know that the pressure of a gas will increase if its temperature increases. The question is: how exactly does the pressure change with temperature? This step makes up the bulk of the stellar model, and it can be as complicated as you can imagine a million-mile wide, blindingly hot, barely stable nuclear reaction being. Scientists spend entire careers writing wildly complicated computer programs to model the dynamics of stars ever more accurately. We’re not going to do that here. We’re going to assume that the relationship between temperature and pressure follows a very simple model known as the ideal gas law. The ideal gas law states that the pressure of a gas is proportional to both its temperature and its density:

$P = KDT$

where $K$ is a proportionality constant (kind of like $G$ for gravity). Density is just defined as the amount of mass per unit volume. (A pound of feathers and a pound of lead may weigh the same, but the pound of lead takes up much less volume, meaning it’s more dense.) Also remember from geometry that the volume of a sphere is $V=\frac{4}{3}\pi R^3$ . So we have:

$D=\frac{M}{V} \text{, and }V=\frac{4}{3}\pi R^3$

$D = \frac{3M}{4\pi R^3}$

So if we combine the relation for density with the one for pressure, we get:

$P = \frac{3KMT}{4\pi R^3}$

Now we have two equations for pressure: one from equating pressure with gravity and one from relating pressure to temperature through the ideal gas law. We can combine these two equations

$P=\frac{GM^2}{4\pi R^4}$

$P = \frac{3KMT}{4\pi R^3}$

to get an equation relating temperature to mass:

$\frac{GM^2}{4\pi R^4} = \frac{3KMT}{4\pi R^3}$

$T=\frac{GM}{3KR}$

Alright, final step. We mentioned before that a star’s luminosity is related to its temperature via the Stefan-Boltzmann law:

$L \propto T^4$

This was a simplified version of the Stefan-Boltzmann law; let’s add in the rest of the equation:

$L = C \frac{R^4T^4}{M}$

The luminosity is related to temperature, mass, and radius of the star. Again, $C$ is a proportionality constant, like $G$ and $K$ before it. Now we can take the equation we found for temperature and stick it in the luminosity equation to get:

$L = C \frac{R^4 G^4 M^4}{3^4 K^4 R^4 M}$

Simplifying:

$L=C \frac{G^4 M^3}{81 K^4}$

This equation shows us that the luminosity is proportional to the cube of the mass of the star, $L \propto M^3$ . Finally, we have an equation that allows us to calculate the mass of a star from the amount of light it gives off. It may seem really roundabout, and it’s really indirect, but that’s how we know how much stars weigh.

Leave a Reply Cancel reply