How do we know that light is a wave?

We seem to know a lot about waves nowadays.  The language of waves suffuses our vernacular:  “We’re on the same wavelength,” “That speech resonates with me,” “I get weird vibes from him,” all use wave terminology.  We’re intimately familiar with water waves:  we see them in the shower or the sink pretty much every day.  We have a pretty good grasp on sound waves:  we can feel bass vibrations pretty easily and if we play music, we know that we can see vibrating waves in the motions of strings and cymbals, or we can feel vibrations of a saxophone reed or a trumpet mouthpiece.  We tend to accept the existence of things like microwaves and radio waves, which are really just light waves that are outside our range of light perception, much as x-rays and UV light are.  And everyone can recite from their science classes that light is an electromagnetic wave.  But what does that mean?  And how do we know it?

To begin, what sorts of things would lead people to believe that light could be a wave in the first place?  What would you even begin to answer if someone asked you, “What is light?”  You might say that it’s a beam of some kind, that it travels in straight lines, that it can be reflected by a mirror.  If someone asked you what light is a beam of, it might take you a little longer to answer.  Bullets, arrows, and rocks travel in lines that are more or less straight over short distances, and they can be reflected off shields and walls, so maybe you would think that light is made up of little shiny bullets.  But it seems like light is more continuous than bullets or arrows, so maybe you would think that a beam of light is like a jet of water or air.  And while it’s true that we are able to see waves made out of water or air, we generally tend to think of a wave as a way that water moves, for example.  We don’t typically think of water as being “made of waves.”  In fact, it’s the other way around.  We tend to think of waves as being made of water (or air, or Jello, or whatever).

So maybe your first thought would be that light is made up of particles like a hail of bullets, or perhaps that light is made up of a fluid, like water or air.  And there have always been a lot of different theories of light, with their supporters and detractors.  Isaac Newton was pretty convinced that light was made out of a stream of particles, which he called corpuscles.  At roughly the same time, Christiaan Huygens, a Dutch mathematician and astronomer, had a competing theory:  that light was made up of waves.  It turns out that Huygens was closer to the truth than Newton, but since Newton was seen as nigh infallible in the 17th century, Huygens’s theory fell into disrepute.  Now, as it turns out, you can think of light as a stream of particles (something we’ll talk about in a future HDWKI), but they don’t behave according to Newton’s laws.  So while Newton ended up being correct in spirit, he was wrong in the details.

It’s important to point out that both Newton and Huygens were able to explain some of the main features of light.  Both theories predicted that light moves at a finite speed, and in fact, both men gave estimates of the speed of light (Huygens underestimated the speed by about 25%; Newton overestimated it by a somewhat smaller amount).  Both theories predicted that light reflected off a mirror at the same angle that it hit it:

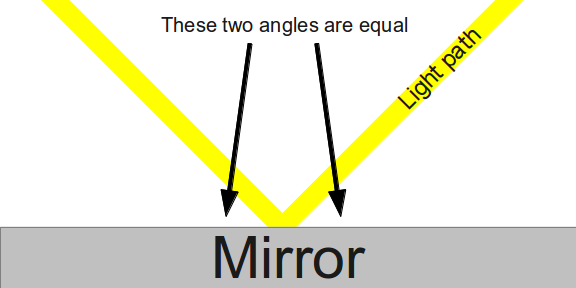Both theories also explained why light seems to bend, or refract, when it passes through different materials:

Newton’s theory of refraction was complex, detailed, and based on scrupulous observation.  He first observed a phenomenon called total internal reflection that anyone who’s ever been in a pool is familiar with.  He noted that, at a shallow enough angle, light could not pass from water into air, but rather was reflected back into the water.  Here’s a picture of the phenomenon:

The reflection of the turtle on the surface of the water is an example of total internal reflection, where light cannot pass from the water into the air above, but rather reflects back into the water.  Newton reasoned that, since air is far less dense than water, it’s not the air that is preventing the light from escaping the water (there’s not much material in the air to exert a force on the light corpuscles).  This meant that the water itself must be exerting some force on the light to prevent the particles from escaping.  Newton then recalled his second law, F=ma, which says that if you apply a force to an object, it accelerates.  He asserted that the water was applying a force to the light corpuscles, and that they were being accelerated.  This meant that their path was bent, which is exactly what he observed when light was refracted.  So Newton actually had a pretty cohesive theory of light.  It’s too bad it was wrong.

There were a few phenomena that Newton’s theory couldn’t handle very well.  One glaring problem was how Newton handled the fact that light could be reflected and transmitted through the same surface.  This effect is familiar to anyone who has looked at a window from the outside:

Notice that you can see blinds and flowerpots through the windows, but you can also see the reflections of trees.  This means that light is both reflected and transmitted through the windows.  Newton accounted for this behavior by saying that each light corpuscle was in a certain “fit.”  If the corpuscle was in a reflective “fit,” it would reflect off surfaces.  If it was in a transmissive “fit,” it would pass through surfaces.  The difficulty with this hypothesis shows up when you pass a light beam through several successive materials.  Some of the light is transmitted and some is reflected at each stage.  In the language of corpuscles, this means that a corpuscle can change back and forth from a reflective fit to a transmissive fit for no apparent reason.

As it turns out, the wave theory of Huygens did a pretty good job explaining the phenomena in the pictures above, without the clunky notion of Newtonian “fits.”  These concepts are best explained in a series of animated gifs (I never thought I’d say that with a straight face), so I’ve prepared a bunch of them for your enjoyment.  The first assumption Huygens made was that light is given off equally in all directions at each point in a glowing object.  If the object consists of only one point, then the light waves look like this:

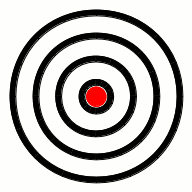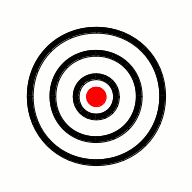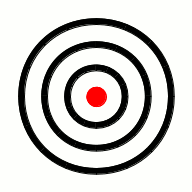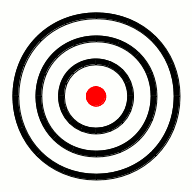If, on the other hand, the glowing object was, e.g., a rod, then each point along the rod would give off light waves independently, like this:

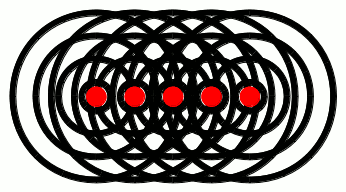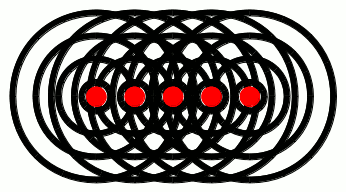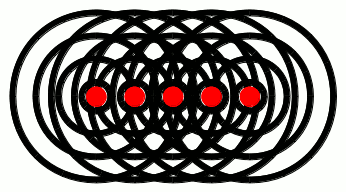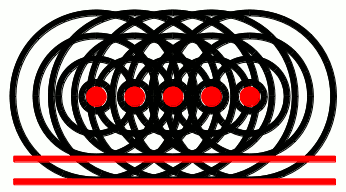Notice how the waves from each point pile up at the red lines.  These lines are called wavefronts, and they pile up on each other because of a phenomenon called interference. We’ve talked about interference extensively in a previous post.  If you haven’t read that post yet, go ahead and take a look at the link:  it’ll help out a lot with the subsequent discussion in this post.  We’ll have more to say about interference in a minute.  For now, just keep in mind that waves can constructively interfere to give wavefronts, as shown in the gif above.  One other thing to note from the animation above:  the direction in which the wavefronts move is perpendicular to the wavefronts themselves.  You’re probably already familiar with this phenomenon yourself, if you’ve ever been to a beach:

We can use these wavefronts to illustrate how light reflects off a mirror:

If we assume that light waves travel in different speeds when moving through different materials, then we can also explain refraction:

Assuming that each point being hit by light radiates waves in all directions, we can imagine that Huygens’s theory explains why light can be reflected and transmitted at the same time, avoiding Newton’s notion of “fits.”  Huygens’s wave theory is elegant, and we’ve examined several points that make it a plausible alternative to Newton’s corpuscles.  But what ultimately convinced the scientific community that the wave theory was right, and Newton’s theory was wrong?

An English scientist named Thomas Young was researching the physics of sound waves in the 1790’s when he noticed that much of the mathematical framework he was using to describe sound could also apply to light.  Young worked on his theory, augmented it with several experiments, and began giving presentations and publishing papers on it in the first decade of the 19th century.  His main result was the observation of interference fringes, also called diffraction patterns:

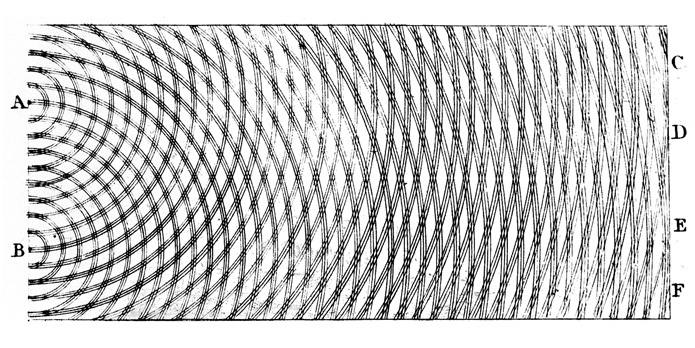
Young assumed, just as we did earlier, that an extended glowing object such as a rod or the face of a mirror, would radiate light waves in all directions, and we would observe light along wavefronts that constructively interfere.  In the picture above, Young proposed the following experiment:  what if we set up a situation where light waves could only radiate from two points (A and B in the picture)?  Then we would get alternating constructive and destructive interference that would cause light beams to radiate out in a characteristic pattern:

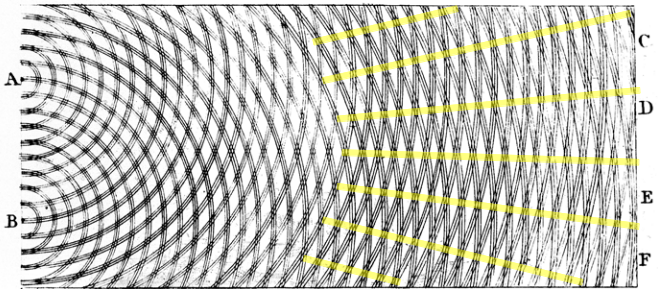To actually carry out this experiment, you need to shine a beam of light on some sort of opaque object with two very small holes or slits in it.  As the light passes through these holes, you then look at the pattern produced on the wall behind the slits.  Here’s an example of what you see:

Young figured out that the spacing between the slits and the wavelength of the light determined the pattern of interference.  He could measure the distance between the slits, and he could observe the interference pattern.  This allowed him to work backwards to get the wavelengths of various colors of light.  He concluded that visible light has a wavelength range from roughly 1/60000th of an inch (for deep violet) to 1/36000th of an inch (for dark red).  How does this compare with what we know today?  When we convert these values to nanometers (1 nanometer, or nm, is 1 billionth of a meter, and this is the standard length scale that scientists use for visible light today), we find that Young predicted visible light to be between roughly 420 and 710 nm.  The current accepted wavelength range for visible light is about 400-700 nm.  So Young was pretty much spot-on, given the natural variability in people’s eyesight.

Young’s work was influential, and cracks were already starting to appear in the facade of Newton’s theory, but the final blow came from a Frenchman by the name of Augustin-Jean Fresnel.  Fresnel took up and extended Young’s wave hypothesis, and in 1818 he entered a paper on diffraction patterns into a contest that was being held by the French Academy of Sciences.  The committee that was tasked with judging the contest consisted of several scientists who adhered strongly to Newton’s corpuscular theory, including Simeon Denis Poisson, an eminent physicist at the time.  Poisson reviewed Fresnel’s paper and noticed that the equations predicted an odd phenomenon.  If a beam of light is shined on a small circular disk, Fresnel’s theory predicted that a small spot should appear directly behind the disk.  To a corpuscular theorist, this is ludicrous.  And in fact, it doesn’t seem to make intuitive sense.  If you block a beam of light, you should make a shadow, not a spot of light.  Poisson gave Fresnel a withering critique, but Fresnel had an ally among the contest judges.  François Arago, himself sympathetic to the wave theory, decided to actually perform the experiment, rather than simply discounting Fresnel’s claim on a theoretical basis.  Arago shined a bright beam of light onto a 2 millimeter target in a very dark room, and to the amazement of everyone, was able to observe the spot that Fresnel’s theory predicted.

After this experiment, Newton’s corpuscular theory was virtually abandoned and the wave theory of light reigned supreme.  Fresnel ended up winning the contest, and Arago and Fresnel would begin a fruitful collaboration that would last the rest of their lives.  And that’s how we know that light is a wave.

References

• The description of Newton’s theory is taken straight from his “Opticks,” a copy of which can be found here.  A brief note: for the example of total internal reflection, Newton actually observed reflection at the interface of glass and vacuum.  I switched the materials to correspond to the picture of the turtle.  I like turtles.
• For the most part, the gifs are adapted from diagrams in Christiaan Huygens’s “Treatise on Light,” a wonderfully illustrated book which can be found here.
• Thomas Young’s work, “A course of lectures on natural philosophy and the mechanical arts,” is available on Google Books here.
• Classic papers by Huygens, Young, Fresnel, and Arago can be found in the collection here.
• Fresnel’s prize winning paper is available in its original French here.  The preface provides background for the Poisson-Fresnel conflict, and Fresnel’s own notes describe Arago’s experiment.