Last time, we looked at the agony and ecstasy of the life of Robert FitzRoy, the world’s first weather forecaster. Like most other weather forecasters, FitzRoy provided an invaluable service, and yet was mocked resoundingly when his forecasts were in error. Unlike most weather forecasters, this criticism drove him deeper into an already deep depression, and he ended up committing suicide only a few years into his new gig. We may empathize with FitzRoy’s plight, but who among us hasn’t at some point been in awe of the sheer inaccuracy of a weather forecast? Why should FitzRoy have it easier than Lady Catherine, Jane Austen’s archetypal ultrarich know-nothing? Of course, this naturally leads us to the question: will we ever be able to make a truly accurate weather forecast? The answer to this question is a big fat no. But the path to that big fat no is quite a bit more interesting than you might expect.
Lorenz doesn’t toe the line
By the 1950’s, scientists had gotten really good at forecasting average properties of the weather using statistical methods (e.g., given a location, how many days on average does it rain in a given month?). But Edward Lorenz didn’t just want to incrementally improve the statistical accuracy of weather forecasts. He wanted to develop an accurate model of the atmosphere, in all its gory detail. Lorenz’s goal might not sound particularly ambitious, but in fact, he was using mathematics to model the weather that was fundamentally different than what other scientists were using.
You see, the scientists that came before Lorenz all used atmospheric models that were linear systems of equations. We’re all familiar with lines, and we might even know that a system of equations is just a group of equations that gives a unique solution. So we might be tempted to think that the scientists before Lorenz were involved in the business of unique line-drawing, or some such thing. But mathematicians mean something a little different when they use the word “linear.” For them, a linear system of equations is one where existing solutions to the equations can be combined to give new solutions. So, yes, lines are a linear system: if you add two lines together, you get a third line. But there are also more complicated linear systems, one of which we’re already quite familiar with: waves. If you remember from our discussion about the X-ray diffraction patterns of diamond and graphite, waves can add together to give various levels of constructive or destructive interference. The important observation here is that when we add two waves together, we get a third wave that is a combination of the first two. This property (which is called superposition), is a characteristic of all linear systems, and was a feature in most weather models before Lorenz.
But the equations which accurately model the flow of air in the atmosphere are not linear (we scientists have a fancy name for systems of equations which are not linear: we call them nonlinear). This means that you can’t take any two configurations of the weather and add them together to get a new weather pattern. Superposition is no longer true for nonlinear systems. You might think that these equations would be more difficult to solve, and in fact they are–tremendously difficult. The scientists before Lorenz had made some assumptions that allowed them to treat the nonlinear equations of the atmosphere as if they were approximately linear. The thought was that the approximations were “good enough,” especially considering how much time they saved over solving the much more difficult nonlinear equations directly. But Lorenz wanted to tackle the problem head on, by having a go at the real nonlinear deal.
How good can weather forecasts get?
Luckily for Lorenz, for the first time in the 1950’s, meteorologists had a new weapon at their disposal: computers. These computers were tens of millions of times slower than modern computers and hundreds of times more expensive, but scientists were beginning to use them nonetheless to crunch through the harrowing maze of differential equations that govern the behavior of our atmosphere.
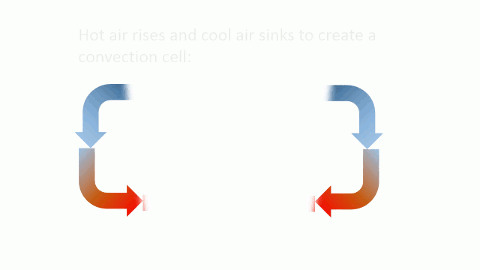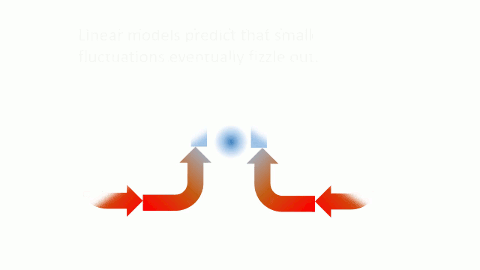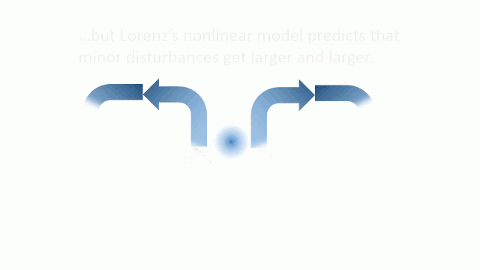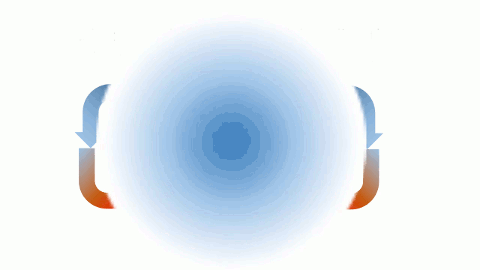
Immediately, Lorenz noticed some quirky behavior in his calculations that suggested earlier scientists’ approximations were certainly not “good enough.” A central feature of his model was that it could accurately predict convection, which is the motion that occurs when hot air rises and cool air sinks. Linear models predict that, over time, convection in the atmosphere will become well-behaved and orderly, which should theoretically make the weather quite easy to predict. Any small fluctuations will be damped out, becoming smaller and smaller until eventually they are inconsequential in the face of large-scale atmospheric processes.
Lorenz noticed something odd when he plugged the full nonlinear equations into the computer. Small fluctuations, which were supposed to eventually dwindle to nothing, were actually amplifying themselves and getting bigger and bigger until they eventually dominated the behavior of the atmosphere. If this were true, then it would mean that it is essentially impossible to predict a precise weather forecast for a given area more than a few weeks in advance. The statistical properties of the weather still hold (e.g., you can predict that Seattle is rainier than Phoenix in general), but the particulars of the weather are completely unpredictable.
What’s more, Lorenz found that the smaller the disturbance, the more quickly it grows in size. In order to disseminate his ideas to a wider audience, Lorenz gave a talk at the annual meeting of the American Association for the Advancement of Science (AAAS) in 1972 entitled “Predictability; Does the Flap of a Butterfly’s wings in Brazil Set Off a Tornado in Texas?” The popular press latched onto this metaphor and dubbed Lorenz’s discovery the butterfly effect. What it means for us is that small fluctuations will grow into large disturbances in the atmosphere over a period of about a month or so, meaning that our weather forecasts can never be accurate more than about two weeks in advance.
Butterflies Everywhere
Weather forecasting is the original, and most easily observable, example of how small fluctuations can feed on themselves and grow to become enormous. But it certainly isn’t the only example. There are plenty of other areas where the butterfly effect shows up, including ecological predator-prey relationships, chemical reactions, turbulence in air and water, as well as certain mechanical and electrical systems. The butterfly effect is actually pretty common in nonlinear systems, and it is an important concept in a branch of math known as chaos theory. We’ll have more to say about this in a future HDWKI.
References
- Lorenz’s first paper describing the chaotic nature of atmospheric convection can be found here.
- An important paper in the development of Lorenz’s theory is found here.
- The announcement and abstract of “Predictability; Does the Flap of a Butterfly’s wings in Brazil Set Off a Tornado in Texas?” can be found here.
- An obituary of Lorenz, written by his colleague Tim Palmer, can be found here.